
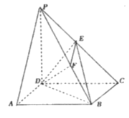
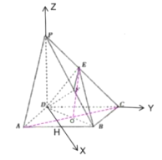
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,侧棱
,侧棱![]() 底面
底面![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,作
的中点,作![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)见解析 (3)![]()
【解析】
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,根据中位线定理证明
,根据中位线定理证明![]() ,即可证得
,即可证得![]() 平面
平面![]() .
.
(2)先证![]() 平面
平面![]() .又∵
.又∵![]() 平面
平面![]() ,则
,则![]() .
.
(3)建立空间直角坐标系,列出各点的坐标表示,求出平面![]() 的法向量为
的法向量为![]() ,又因
,又因![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的一条法向量,利用余弦公式求解即可得出二面角
的一条法向量,利用余弦公式求解即可得出二面角![]() 的余弦值.
的余弦值.
解:(1)证明:连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
因为![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中位线
的中位线
∴![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]()
(2)在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,
∴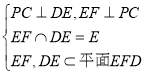 ,则
,则![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,则
,则![]() .
.
(3)取![]() 中点
中点![]() ,连接
,连接![]() .
.
依题意可得![]() 为等边三角形,∴
为等边三角形,∴![]() ,
,![]()
又因为![]() 底面
底面![]() ,
,![]() ,
,![]() 平面
平面![]()
则![]() ,
,![]()
建立以![]() 为坐标原点,如图所示坐标系,则有:
为坐标原点,如图所示坐标系,则有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
则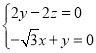
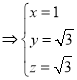 ,∴
,∴![]()
∵![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的一条法向量,且
的一条法向量,且![]()
∴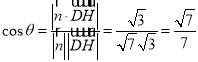


科目:高中数学 来源: 题型:
【题目】某地举行水上运动会,如图,岸边有![]() 两点,
两点,![]() ,小船从
,小船从![]() 点以
点以![]() 千米/小时的速度沿
千米/小时的速度沿![]() 方向匀速直线行驶,同一时刻运动员出发,经过
方向匀速直线行驶,同一时刻运动员出发,经过![]() 小时与小船相遇.(水流速度忽略不计)
小时与小船相遇.(水流速度忽略不计)
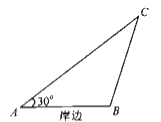
(1)若![]() ,
,![]() ,运动员从
,运动员从![]() 处出发游泳匀速直线追赶,为保证在1小时内(含1小时)能与小船相遇,试求运动员游泳速度的最小值;
处出发游泳匀速直线追赶,为保证在1小时内(含1小时)能与小船相遇,试求运动员游泳速度的最小值;
(2)若运动员先从![]() 处沿射线
处沿射线![]() 方向在岸边跑步匀速行进
方向在岸边跑步匀速行进![]() 小时后,再游泳匀速直线追赶小船.已知运动员在岸边跑步的速度为4千米小时,在水中游泳的速度为2千米小时,试求小船在能与运动员相遇的条件下
小时后,再游泳匀速直线追赶小船.已知运动员在岸边跑步的速度为4千米小时,在水中游泳的速度为2千米小时,试求小船在能与运动员相遇的条件下![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在非零常数
,如果存在非零常数![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是“似周期函数”,非零常数
是“似周期函数”,非零常数![]() 为函数
为函数![]() 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”![]() 的“似周期”为
的“似周期”为![]() ,那么它是周期为2的周期函数;
,那么它是周期为2的周期函数;
②函数![]() 是“似周期函数”;
是“似周期函数”;
③如果函数![]() 是“似周期函数”,那么“
是“似周期函数”,那么“![]() 或
或![]() ”.
”.
以上正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,左顶点为
,左顶点为![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上的动点,
是椭圆上的动点,![]() 的面积的最大值为
的面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,线段
,线段![]() 的中垂线为
的中垂线为![]() .若直线
.若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记![]() 表示1台机器在三年使用期内的维修次数,
表示1台机器在三年使用期内的维修次数,![]() 表示1台机器在维修上所需的费用(单位:元),
表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求
”的频率不小于0.8,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,点
,点![]() 分别为椭圆
分别为椭圆![]() 与坐标轴的交点,且
与坐标轴的交点,且![]() .过
.过![]() 轴上定点
轴上定点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为线段
为线段![]() 的中点.
的中点.
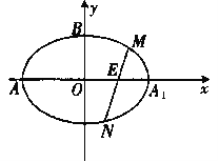
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,椭圆
,椭圆![]() 的离心率是
的离心率是![]() ,
,![]() 的面积是
的面积是![]() .
.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() 点),若直线
点),若直线![]() 与直线
与直线![]() 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com