
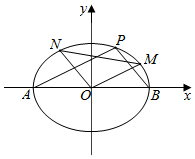
 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(1,$\frac{\sqrt{6}}{2}$),且离心率等于$\frac{\sqrt{2}}{2}$.点A,B分别为椭圆C的左、右顶点,M,N是椭圆C上非顶点的两点,且△OMN的面积等于$\sqrt{2}$.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(1,$\frac{\sqrt{6}}{2}$),且离心率等于$\frac{\sqrt{2}}{2}$.点A,B分别为椭圆C的左、右顶点,M,N是椭圆C上非顶点的两点,且△OMN的面积等于$\sqrt{2}$.分析 (Ⅰ)运用椭圆的离心率公式和点满足椭圆方程,以及a,b,c的关系,解得a,b,即可得到椭圆方程;
(Ⅱ)解法一、设直线OM,ON的方程为y=kOMx,y=kONx,代入椭圆方程,求得M,N的坐标,求出△OMN的面积,由条件可得${k_{OM}}{k_{ON}}=-\frac{1}{2}$.设P(xP,yP),则$4-x_P^2=2y_P^2$,又已知kAP=kOM,即证kBP=kON即可;
解法二、设直线AP的方程为y=kOM(x+2),代入x2+2y2=4,求出P的坐标和BP的斜率,所以只需证$-\frac{1}{{2{k_{OM}}}}={k_{ON}}$,即${k_{OM}}{k_{ON}}=-\frac{1}{2}$,即可得到证明.
解答 解:(Ⅰ)由题意得,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,a2-b2=c2,
代入点(1,$\frac{\sqrt{6}}{2}$),可得$\frac{1}{{a}^{2}}$+$\frac{3}{2{b}^{2}}$=1,
解得,a=2,b=$\sqrt{2}$,
故椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1;
(Ⅱ)解法一:如图所示,设直线OM,ON的方程为y=kOMx,y=kONx,
联立方程组$\left\{\begin{array}{l}y={k_{OM}}x\\ \frac{x^2}{4}+\frac{y^2}{2}=1\end{array}\right.$,解得$M(\frac{2}{{\sqrt{1+2k_{OM}^2}}},\frac{{2{k_{OM}}}}{{\sqrt{1+2k_{OM}^2}}})$,
同理可得$N(-\frac{2}{{\sqrt{1+2k_{ON}^2}}},-\frac{{2{k_{ON}}}}{{\sqrt{1+2k_{ON}^2}}})$,
作MM'⊥x轴,NN'⊥x轴,M',N'是垂足,
S△OMN=S梯形MM'N'N-S△OMM'-S△ONN'=$\frac{1}{2}[({y_M}+{y_N})({x_M}-{x_N})-{x_M}{y_M}+{x_N}{y_N}]$
=$\frac{1}{2}({x_M}{y_N}-{x_N}{y_M})$=$\frac{1}{2}(\frac{{-4{k_{ON}}}}{{\sqrt{1+2{k^2}_{OM}}\sqrt{1+2{k^2}_{ON}}}}+\frac{{4{k_{OM}}}}{{\sqrt{1+2{k^2}_{OM}}\sqrt{1+2{k^2}_{ON}}}})$
=$\frac{{2({k_{OM}}-{k_{ON}})}}{{\sqrt{1+2{k^2}_{OM}}\sqrt{1+2{k^2}_{ON}}}}$,
已知S△OMN=$\sqrt{2}$,化简可得${k_{OM}}{k_{ON}}=-\frac{1}{2}$.
设P(xP,yP),则$4-x_P^2=2y_P^2$,
又已知kAP=kOM,所以要证kBP=kON,
只要证明${k_{AP}}{k_{BP}}=-\frac{1}{2}$,
而${k_{AP}}{k_{BP}}=\frac{y_P}{{{x_P}+2}}\frac{y_P}{{{x_P}-2}}=\frac{{{y^2}_P}}{{{x^2}_P-4}}=-\frac{1}{2}$,
所以可得BP∥ON.
(M,N在y轴同侧同理可得).
解法二:设直线AP的方程为y=kOM(x+2),代入x2+2y2=4,
得$(2k_{OM}^2+1){x^2}+8k_{OM}^2x+8k_{OM}^2-4=0$,它的两个根为-2和xP,
可得${x_p}=\frac{{2-4k_{OM}^2}}{{2k_{OM}^2+1}}$,${y_P}=\frac{{4{k_{OM}}}}{{2k_{OM}^2+1}}$,
从而${k_{BP}}=\frac{{\frac{{4{k_{OM}}}}{{2k_{OM}^2+1}}}}{{\frac{{2-4k_{OM}^2}}{{2k_{OM}^2+1}}-2}}=-\frac{1}{{2{k_{OM}}}}$,
所以只需证$-\frac{1}{{2{k_{OM}}}}={k_{ON}}$,即${k_{OM}}{k_{ON}}=-\frac{1}{2}$,
设M(x1,y1),N(x2,y2),若直线MN的斜率不存在,易得x1=x2=±$\sqrt{3}$,
从而可得kOMkON=-$\frac{3}{2}$,
若直线MN的斜率存在,设直线MN的方程为y=kx+m,
代入$\frac{x^2}{4}+\frac{y^2}{2}=1$
得(2k2+1)x2+4kmx+2m2-4=0,
则${x_1}+{x_2}=-\frac{4km}{{2{k^2}+1}}$,${x_1}{x_2}=\frac{{2{m^2}-4}}{{2{k^2}+1}}$,△=8(4k2+2-m2)>0,${S_{△OMN}}=\frac{1}{2}|m|•|{x_1}-{x_2}|=\frac{1}{2}|m|•\frac{{\sqrt{8(4{k^2}+2-{m^2})}}}{{2{k^2}+1}}=\sqrt{2}$,
化得m4-(4k2+2)m2+(2k2+1)2=0,得m2=2k2+1,${k_{OM}}•{k_{ON}}=\frac{{{y_1}{y_2}}}{{{x_1}{x_2}}}=\frac{{{k^2}{x_1}{x_2}+km({x_1}+{x_2})+{m^2}}}{{{x_1}{x_2}}}=\frac{{{m^2}-4{k^2}}}{{2{m^2}-4}}=\frac{{2{k^2}+1-4{k^2}}}{{2(2{k^2}+1)-4}}=-\frac{1}{2}$.
故BP∥ON.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和点满足椭圆方程,考查直线平行的证明,注意运用直线方程和椭圆方程联立,求得交点,考查化简整理的运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
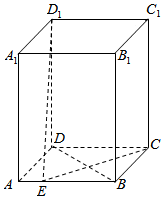 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱AA1⊥底面ABCD,已知AB=1,${A}{{A}_1}=\sqrt{3}$,E为AB上一个动点,则D1E+CE的最小值为( )
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱AA1⊥底面ABCD,已知AB=1,${A}{{A}_1}=\sqrt{3}$,E为AB上一个动点,则D1E+CE的最小值为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{10}$ | C. | $\sqrt{5}+1$ | D. | $2+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com