
如图,正方形CDEF内接于椭圆 ,且它的四条边与坐标轴平行,正方形GHPQ的顶点G,H在椭圆上,顶点P,Q在正方形的边EF上.且CD=2PQ=
,且它的四条边与坐标轴平行,正方形GHPQ的顶点G,H在椭圆上,顶点P,Q在正方形的边EF上.且CD=2PQ= .
.

(1)求椭圆的方程;
(2)已知点M(2,1),平行于OM的直线l在y轴上的截距为m(m:≠0),l交椭圆于A,B两个不同点,求证:直线MA,MB与x轴始终围成一个等腰三角形.
(1)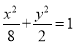 ;(2)证明过程详见解析.
;(2)证明过程详见解析.
【解析】
试题分析:本题主要考查椭圆的标准方程、直线与椭圆相交问题等数学知识,考查学生分析问题解决问题的能力和计算能力.第一问,由图形分析,利用CD和PQ的边长得出点E和点G的坐标,由于这2点都在椭圆上,联立方程得出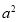 和
和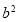 ,从而得到椭圆的标准方程;第二问,通过对题意的分析,只需证明直线MA,MB的斜率之和为0即可,设出A,B点坐标,列出2条直线的斜率
,从而得到椭圆的标准方程;第二问,通过对题意的分析,只需证明直线MA,MB的斜率之和为0即可,设出A,B点坐标,列出2条直线的斜率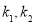 的表达式,直线
的表达式,直线 与椭圆方程联立消参,得到关于x的方程,列出两根之和与两根之积,而
与椭圆方程联立消参,得到关于x的方程,列出两根之和与两根之积,而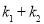 通过转化可以将得到的两根之和与两根之积代入,只要最后化简结果为0即可.
通过转化可以将得到的两根之和与两根之积代入,只要最后化简结果为0即可.
试题解析:(1)∵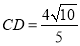 ,∴点
,∴点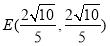 ,
,
又∵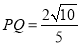 ,∴点
,∴点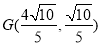 ,
,
则 ,解得
,解得 ,
,
∴椭圆方程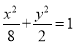 .(4分)
.(4分)
(2)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可,设A(x1,y1),B(x2,y2),则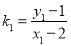 ,
,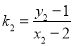 ,直线l方程为
,直线l方程为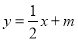 ,代入椭圆方程
,代入椭圆方程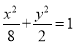 消去y,
消去y,
得x2+2mx+2m2-4=0可得x1+x2=-2m,x1x2=2m2-4.(9分)
而
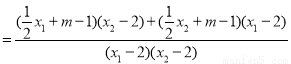
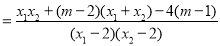
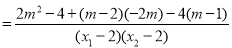
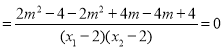 ,(12分)
,(12分)
∴k1+k2=0,故直线MA、MB与x轴始终围成一个等腰三角形.(13分)
考点:1.椭圆的标准方程;2.韦达定理.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源:2013-2014学年陕西省高三第六次模拟理科数学试卷(解析版) 题型:选择题
“ ”是“函数
”是“函数 存在零点”的
存在零点”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年重庆市高三下学期考前模拟(二诊)理科数学试卷(解析版) 题型:选择题
如图是收集重庆市2013年9月各气象采集点处的平均气温(单位:℃)的数据制成的频率分布直方图,图中有一处因污迹看不清。已知各采集点的平均气温范围是 ,且平均气温低于22.5℃的采集点个数为11,则平均气温不低于25.5℃的采集点个数为( )
,且平均气温低于22.5℃的采集点个数为11,则平均气温不低于25.5℃的采集点个数为( )

(A)6 (B)7 (C)8 (D)9
查看答案和解析>>
科目:高中数学 来源:2013-2014学年重庆市高三下学期考前模拟(二诊)文科数学试卷(解析版) 题型:选择题
设 是椭圆
是椭圆 上两点,点
上两点,点 关于
关于 轴的对称点为
轴的对称点为 (异于点
(异于点 ),若直线
),若直线 分别交
分别交 轴于点
轴于点 ,则
,则 ( )
( )
(A)0 (B)1 (C) (D)2
(D)2
查看答案和解析>>
科目:高中数学 来源:2015届北京市高三上学期期中考试理科数学试卷(解析版) 题型:填空题
定义在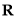 上的函数
上的函数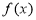 ,如果存在函数
,如果存在函数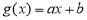 (
(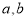 为常数),使得
为常数),使得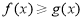 对一切实数
对一切实数 都成立,则称
都成立,则称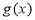 为函数
为函数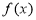 的一个承托函数.给出如下命题:
的一个承托函数.给出如下命题:
①函数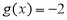 是函数
是函数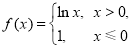 的一个承托函数;
的一个承托函数;
②函数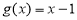 是函数
是函数 的一个承托函数;
的一个承托函数;
③若函数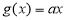 是函数
是函数 的一个承托函数,则
的一个承托函数,则 的取值范围是
的取值范围是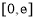 ;
;
④值域是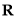 的函数
的函数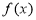 不存在承托函数;
不存在承托函数;
其中,所有正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古巴彦淖尔市高三10月月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.

求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com