
(本小题满分12分)如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.

求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
(1)见解析;(2)见解析.
【解析】
试题分析:(1)要证直线EF∥平面PCD,只需证EF和平面PCD内的一条直线平行,在三角形PAD中易知EF∥PD得证;(2)要证面面垂直,只需证其中一个面BEF中的一条线垂直于另一平面PAD,根据已知条件知BF⊥AD,又有平面PAD⊥平面ABCD,BF?平面ABCD,平面PAD∩平面ABCD=AD,所以BF⊥平面PAD,所以平面BEF⊥平面PAD.
试题解析:(1)在△PAD中,因为E,F分别为AP,AD的中点,所以EF∥PD.
又因为EF ?平面PCD,PD?平面PCD,所以直线EF∥平面PCD.
连接BD.因为AB=AD,∠BAD=60°,所以△ABD为正三角形.
因为F是AD的中点,所以BF⊥AD.
因为平面PAD⊥平面ABCD,BF?平面ABCD,
平面PAD∩平面ABCD=AD,所以BF⊥平面PAD.
又因为BF?平面BEF,所以平面BEF⊥平面PAD.
考点:1、线面平行的判定;2、面面垂直的判定.


科目:高中数学 来源:2013-2014学年福建省龙岩市高三上学期期末考试理科数学试卷(解析版) 题型:解答题
如图,正方形CDEF内接于椭圆 ,且它的四条边与坐标轴平行,正方形GHPQ的顶点G,H在椭圆上,顶点P,Q在正方形的边EF上.且CD=2PQ=
,且它的四条边与坐标轴平行,正方形GHPQ的顶点G,H在椭圆上,顶点P,Q在正方形的边EF上.且CD=2PQ= .
.

(1)求椭圆的方程;
(2)已知点M(2,1),平行于OM的直线l在y轴上的截距为m(m:≠0),l交椭圆于A,B两个不同点,求证:直线MA,MB与x轴始终围成一个等腰三角形.
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古巴彦淖尔市高三10月月考理科数学试卷(解析版) 题型:选择题
已知函数 的图像与x轴恰有两个公共点,则c= ( )
的图像与x轴恰有两个公共点,则c= ( )
A.-2或2 B.-9或3 C.-1或1 D.-3或1
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古巴彦淖尔市高三10月月考文科数学试卷(解析版) 题型:选择题
已知定义在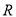 上的函数
上的函数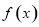 ,对任意
,对任意 ,都有
,都有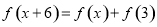 成立,若函数
成立,若函数 的图象关于直线
的图象关于直线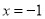 对称,则
对称,则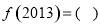
A.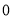 B.
B.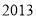 C.
C.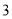 D.
D.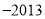
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com