
| A. | -5 | B. | 5 | C. | $-\sqrt{5}$ | D. | $\sqrt{5}$ |
分析 根据题目条件得出$\overrightarrow{a}$$•\overrightarrow{b}$=1×2×cos120°=-1,展开$(\vec a+2\vec b)•(2\vec a+\vec b)$=2|$\overrightarrow{a}$|2$+2|\overrightarrow{b}|$2$+5\overrightarrow{a}$$•\overrightarrow{b}$,即可求解.
解答 解:∵$|\vec a|=1,|\vec b|=2$,$\vec a$与$\vec b$的夹角为120°,
∴$\overrightarrow{a}$$•\overrightarrow{b}$=1×2×cos120°=-1,
∴2×12+2×22+(-5)=5,
故选:B.
点评 本题考察了平面向量的运算,向量的混合运算,数量积的运用,属于基础题,准确化简计算即可.


科目:高中数学 来源: 题型:选择题
| A. | a=7,b=14,A=30°△ABC有两解 | B. | a=9,c=10,A=60°△ABC无解 | ||
| C. | a=6,b=9,A=45°△ABC有两解 | D. | a=30,b=25,A=150°△ABC有一解 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
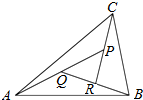 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}$=$\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点恰为P,则$\overrightarrow{AP}$等于( )| A. | $\frac{1}{2}(\overrightarrow a+\overrightarrow b)$ | B. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | C. | $\frac{2}{7}\overrightarrow a+\frac{4}{7}\overrightarrow b$ | D. | $\frac{4}{7}\overrightarrow a+\frac{2}{7}\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 关注NBA | 不关注NBA | 合计 | |
| 男生 | 6 | ||
| 女生 | 10 | ||
| 合计 | 48 |
| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 60.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com