
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 2 | 1 | 3 | 3 | 4 |
| A. | (1,0) | B. | (2,2) | C. | ($\frac{7}{2}$,$\frac{13}{6}$) | D. | (3,1) |
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
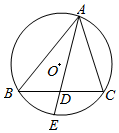 如图,⊙O是△ABC的外接圆,AD平分∠BAC交BC于D,交△ABC的外接圆于E.
如图,⊙O是△ABC的外接圆,AD平分∠BAC交BC于D,交△ABC的外接圆于E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的侧面PAD是正三角形,底面ABCD为菱形,A点E为AD的中点,若BE=PE.
如图,四棱锥P-ABCD的侧面PAD是正三角形,底面ABCD为菱形,A点E为AD的中点,若BE=PE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患心肺疾病 | 不患心肺疾病 | 合计 | |
| 大于40岁 | 16 | ||
| 小于或等于40岁 | 12 | ||
| 合计 | 80 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正四棱锥S-ABCD的底面边长为2,E,F分别为SA,SD的中点.
如图,正四棱锥S-ABCD的底面边长为2,E,F分别为SA,SD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com