
【题目】
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知acosC+ccosA=2bcosA.
(1)求角A的值;
(2)求sinB+sinC的取值范围.
【答案】(1)![]() ;(2)
;(2)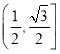 .
.
【解析】
试题(1)要求解,已知条件中有角有边,一般情况下我们可以利用正弦定理把边化为角的关系,本题acosC+ccosA=2bcosA,由正弦定理可化为![]() ,于是有
,于是有![]() ,即
,即![]() ,而
,而![]() ,于是
,于是![]() ,
,![]() ;(2)由(1)
;(2)由(1)![]() ,且
,且![]() ,
,![]() ,由两角和与差的正弦公式可转化为
,由两角和与差的正弦公式可转化为![]() ,再由正弦函数的性质可得取值范围.
,再由正弦函数的性质可得取值范围.
试题解析:(1)因为acosC+ccosA=2bcosA,所以sinAcosC+sinCcosA=2sinBcosA,
即sin(A+C)=2sinBcosA.
因为A+B+C=π,所以sin(A+C)=sinB.
从而sinB=2sinBcosA.
因为sinB≠0,所以![]()
因为0<A<π,所以![]()
(2)![]()
因为![]() ,所以
,所以![]() .
.
所以sinB+sinC的取值范围为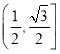 .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图是正方体的平面展开图,在这个正方体中;
(1)BM与ED平行;(2)CN与BE是异面直线;(3)CN与BM所成角为60°;(4)CN与AF垂直. 以上四个命题中,正确命题的序号是( )
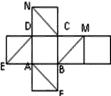
A.(1)(2)(3)B.(2)(4)C.(3)(4)D.(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() .
.
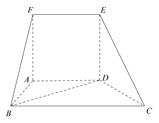
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家鞋帽商场销售同一批品牌运动鞋,每双标价为800元,甲、乙两商场销售方式如下:在甲商场买一双售价为780元,买两双每双售价为760元,依次类排,每多买一双则所买各双售价都再减少20元,但每双售价不能低于440元;乙商场一律按标价的75%销售.
(1)分别写出在甲、乙两商场购买![]() 双运动鞋所需费用的函数解析式
双运动鞋所需费用的函数解析式![]() 和
和![]() ;
;
(2)某单位需购买一批此类品牌运动鞋作为员工福利,问:去哪家商场购买花费较少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是平行四边形,
是平行四边形,![]() ,
,![]() 为
为![]() 的中点,且有
的中点,且有![]() ,现以
,现以![]() 为折痕,将
为折痕,将![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,且
的位置,且![]()
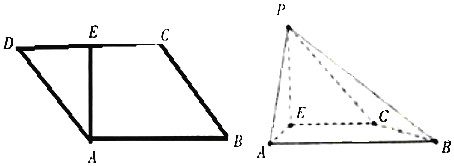
(1)证明:![]() 平面
平面![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的侧面积.
的侧面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com