练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图是正方体的平面展开图，在这个正方体中；

    （1）BM与ED平行；（2）CN与BE是异面直线；（3）CN与BM所成角为60°；（4）CN与AF垂直. 以上四个命题中，正确命题的序号是（ ）

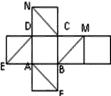
    A.（1）（2）（3）B.（2）（4）C.（3）（4）D.（3）

    【答案】C

    【解析】

    将正方体的展开图复原为正方体，结合图形，逐项判定，即可求解，得到答案.

    由题意，把正方体的展开图复原为正方体，如图所示，结合图形，可得：

    （1）中，与是异面直线，所以与不是平行线，所以不正确；

    （2）中，与是平行直线，所以与不是异面直线，所以不正确；

    （3）中，在正方体中，连接，则，所以与所成的角，即为相交直线与所成的角，在等边三角形中，，即异面直线与所成的角为，所以是正确的；

    （4）中，连接，在正方体中，，

    又由，所以与垂直，所以是正确的.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】甲、乙两人进行射击比赛，各射击局，每局射击次，射击命中目标得分，未命中目标得分，两人局的得分情况如下：

    甲

    乙

    （Ⅰ）若从甲的局比赛中，随机选取局，求这局的得分恰好相等的概率．

    （Ⅱ）如果，从甲、乙两人的局比赛中随机各选取局，记这局的得分和为，求的分布列和数学期望．

    （Ⅲ）在局比赛中，若甲、乙两人的平均得分相同，且乙的发挥更稳定，写出的所有可能取值．（结论不要求证明）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数的反函数为，若存在函数使得对函数定义域内的任意都有，则称函数为函数的“Inverse”函数.

    （1）判断下列哪个函数是函数的“Inverse”函数并说明理由.

    ①；②；

    （2）设函数存在反函数，证明函数存在唯一的“Inverse”函数的充要条件是函数的值域为；

    （3）设函数存在反函数，函数为的一个“Inverse”函数，记，其中，若对函数定义域内的任意都有，求所有满足条件的函数的解析式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在实数集中，定义两个实数、的运算法则△如下：若，则，若，则.

    （1）请分别计算和的值；

    （2）对于实数，判断是否恒成立，并说明理由；

    （3）求函数的解析式，其中，并求函数的最值.（符号“”表示相乘）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某电视台为宣传本省，随机对本省内岁的人群抽取了n人，回答问题“本省内著名旅游景点有哪些”统计结果如图表所示

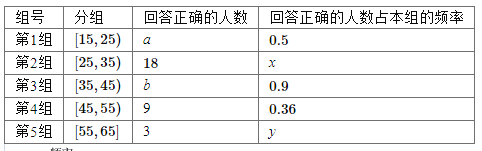
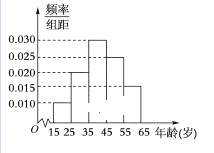
    （1）分别求出的值；

    （2）从第组回答正确的人中用分层抽样的方法抽取6人，求第组每组各抽取多少人？

    （3）指出直方图中，这组数据的中位数是多少（取整数值）？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列命题:

    ①存在实数x,使得sin x+cos x=2；

    ②函数y=cos是奇函数；

    ③若角α,β是第一象限角,且α＜β,则tan α<tan β；

    ④函数y=sin的图象关于点（，0）成中心对称.

    ⑤直线x=是函数y=sin图象的一条对称轴;

    其中正确的命题是(　　 ).

    A.②④B.①③C.①④D.②⑤

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】旅行社为某旅行团包飞机去旅游，其中旅行社的包机费为15000元.旅游团中的每人的飞机票按以下方式与旅行社结算：若旅游团的人数不超过35人时，飞机票每张收费800元；若旅游团的人数多于35人，则给予优惠，每多1人，机票费每张减少10元，但旅游团的人数最多有60人.设旅行团的人数为人，飞机票价格为元，旅行社的利润为元.

    （1）写出飞机票价格元与旅行团人数之间的函数关系式；

    （2）当旅游团的人数为多少时，旅行社可获得最大利润？求出最大利润.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    在△ABC中，内角A，B，C所对的边分别为a，b，c．已知acosC＋ccosA＝2bcosA．

    （1）求角A的值；

    （2）求sinB＋sinC的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对数函数g（x）=1ogax（a＞0，a≠1）和指数函数f（x）=ax（a＞0，a≠1）互为反函数．已知函数f（x）=3x，其反函数为y=g（x）．

    （Ⅰ）若函数g（kx2+2x+1）的定义域为R，求实数k的取值范围；

    （Ⅱ）若0＜x1＜x2且|g（x1）|=|g（x2）|，求4x1+x2的最小值；

    （Ⅲ）定义在I上的函数F（x），如果满足：对任意x∈I，总存在常数M＞0，都有-M≤F（x）≤M成立，则称函数F（x）是I上的有界函数，其中M为函数F（x）的上界．若函数h（x）=，当m≠0时，探求函数h（x）在x∈[0，1]上是否存在上界M，若存在，求出M的取值范围，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案