
【题目】设函数![]() 的反函数为
的反函数为![]() ,若存在函数
,若存在函数![]() 使得对函数
使得对函数![]() 定义域内的任意
定义域内的任意![]() 都有
都有![]() ,则称函数
,则称函数![]() 为函数
为函数![]() 的“Inverse”函数.
的“Inverse”函数.
(1)判断下列哪个函数是函数![]() 的“Inverse”函数并说明理由.
的“Inverse”函数并说明理由.
①![]() ;②
;②![]() ;
;
(2)设函数![]() 存在反函数
存在反函数![]() ,证明函数
,证明函数![]() 存在唯一的“Inverse”函数的充要条件是函数
存在唯一的“Inverse”函数的充要条件是函数![]() 的值域为
的值域为![]() ;
;
(3)设函数![]() 存在反函数
存在反函数![]() ,函数
,函数![]() 为
为![]() 的一个“Inverse”函数,记
的一个“Inverse”函数,记![]() ,其中
,其中![]() ,若对函数
,若对函数![]() 定义域内的任意
定义域内的任意![]() 都有
都有![]() ,求所有满足条件的函数
,求所有满足条件的函数![]() 的解析式.
的解析式.
【答案】(1)②是函数f(x)=log2x的“Inverse”函数,理由见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)分别判断①和②是否满足![]() 即可得到结果;
即可得到结果;
(2)先证充分性,若函数![]() 的值域为
的值域为![]() ,设其定义域为D,则函数
,设其定义域为D,则函数![]() 的定义域为
的定义域为![]() ,值域为D, 令
,值域为D, 令![]() ,
,![]() ,判断是否满足
,判断是否满足![]() ,证明其存在性,再设函数
,证明其存在性,再设函数![]() 和
和![]() 都为函数
都为函数![]() 的“Inverse”函数且不相同,利用反证法证明唯一性;再证必要性,若函数
的“Inverse”函数且不相同,利用反证法证明唯一性;再证必要性,若函数![]() 存在唯一的“Inverse”函数,同样利用反证法,假设函数
存在唯一的“Inverse”函数,同样利用反证法,假设函数![]() 的值域为
的值域为![]() ,令
,令 ,
, ,通过证明函数
,通过证明函数![]() 和
和![]() 都为函数
都为函数![]() 的“Inverse”函数且不相同,这与唯一性矛盾,从而得证;
的“Inverse”函数且不相同,这与唯一性矛盾,从而得证;
(3)由(2)知,![]() 是
是![]() 的一个“Inverse”函数,易得,
的一个“Inverse”函数,易得,![]() ,即
,即![]() ,根据一一对应的性质可得
,根据一一对应的性质可得![]() ,所以
,所以![]() .
.
(1)易得![]() ,对于①,
,对于①,![]() ,故①不是,
,故①不是,
对于②,![]() ,故②是函数
,故②是函数![]() 的“Inverse”函数;
的“Inverse”函数;
(2)先证充分性,若函数![]() 的值域为
的值域为![]() ,设其定义域为D,
,设其定义域为D,
则函数![]() 的定义域为
的定义域为![]() ,值域为D,
,值域为D,
令![]() ,
,![]() ,
,
则对任意![]() 都有,
都有,![]() ,
,
故函数![]() 为函数
为函数![]() 的“Inverse”函数,存在性得证;
的“Inverse”函数,存在性得证;
设函数![]() 和
和![]() 都为函数
都为函数![]() 的“Inverse”函数且不相同,
的“Inverse”函数且不相同,
则存在![]() ,
,![]() ,
,![]() ,且
,且![]() ,因为
,因为![]() 的值域为
的值域为![]() ,
,
故存在![]() ,使得
,使得![]() ,即
,即![]() ,
,![]() ,
,
则![]() ,矛盾,故唯一性得证.
,矛盾,故唯一性得证.
所以函数![]() 存在唯一的“Inverse”函数.
存在唯一的“Inverse”函数.
再证必要性,若函数![]() 存在唯一的“Inverse”函数,
存在唯一的“Inverse”函数,
即存在唯一的函数![]() 满足
满足![]() ,下面用反证法证明必要性.
,下面用反证法证明必要性.
假设函数![]() 的值域为
的值域为![]() ,
,
令 ,
, ,
,
则对任意![]() 都有,
都有,![]() ,
,
且![]() ,
,![]() ,
,
函数![]() 和
和![]() 都为函数
都为函数![]() 的“Inverse”函数且不相同,这与唯一性矛盾,
的“Inverse”函数且不相同,这与唯一性矛盾,
所以函数![]() 的值域为
的值域为![]() ,必要性得证.
,必要性得证.
综上,函数![]() 存在唯一的“Inverse”函数的充要条件是函数
存在唯一的“Inverse”函数的充要条件是函数![]() 的值域为
的值域为![]() ;
;
(3)由(2)知,![]() 是
是![]() 的一个“Inverse”函数,
的一个“Inverse”函数,
由反函数的性质可知,![]() 和
和![]() 都是一一对应的.
都是一一对应的.
则![]() ,
,
又![]() ,则
,则![]() ,
,
即![]() ,根据一一对应的性质可得
,根据一一对应的性质可得![]() ,
,
则![]() ,所以满足条件的函数
,所以满足条件的函数![]() 的解析式为
的解析式为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点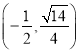 ,且离心率为
,且离心率为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 的右顶点,探究:
的右顶点,探究: ![]() 是否为定值,若是,求出该定值,若不是,请说明理由.(其中,
是否为定值,若是,求出该定值,若不是,请说明理由.(其中, ![]() ,
, ![]() 分别是直线
分别是直线![]() 、
、![]() 的斜率)
的斜率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,根据经验,其次品率![]() 与日产量
与日产量![]() (万件)之间满足关系,
(万件)之间满足关系, (其中
(其中![]() 为常数,且
为常数,且![]() ,已知每生产1万件合格的产品以盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如
,已知每生产1万件合格的产品以盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如![]() 表示每生产10件产品,有1件次品,其余为合格品).
表示每生产10件产品,有1件次品,其余为合格品).
(1)试将生产这种产品每天的盈利额![]() (万元)表示为日产量
(万元)表示为日产量![]() (万件)的函数;
(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是正方体的平面展开图,在这个正方体中;
(1)BM与ED平行;(2)CN与BE是异面直线;(3)CN与BM所成角为60°;(4)CN与AF垂直. 以上四个命题中,正确命题的序号是( )
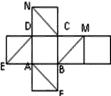
A.(1)(2)(3)B.(2)(4)C.(3)(4)D.(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家鞋帽商场销售同一批品牌运动鞋,每双标价为800元,甲、乙两商场销售方式如下:在甲商场买一双售价为780元,买两双每双售价为760元,依次类排,每多买一双则所买各双售价都再减少20元,但每双售价不能低于440元;乙商场一律按标价的75%销售.
(1)分别写出在甲、乙两商场购买![]() 双运动鞋所需费用的函数解析式
双运动鞋所需费用的函数解析式![]() 和
和![]() ;
;
(2)某单位需购买一批此类品牌运动鞋作为员工福利,问:去哪家商场购买花费较少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com