
【题目】如图,在四棱锥![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点.
的中点.
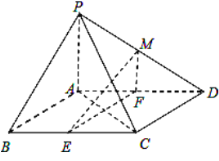
(1)求证:![]() 面
面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
【答案】(1)见解析;(2)![]()
【解析】
(1)由题意得EF⊥AP,AB⊥AC,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,从而四边形ABEF为平行四边形,AB∥EF,进而AC⊥EF,由此能证明EF⊥面PAC.
的中点,从而四边形ABEF为平行四边形,AB∥EF,进而AC⊥EF,由此能证明EF⊥面PAC.
(2)连接AE,AM,推导出AE⊥BC,AE⊥AD,AE⊥PA,从而AE⊥平面PAD,进而∠EMA是EM与平面PAD所成的角,由此能求出直线ME与平面PAD所成角.
(1)证明:∵PA⊥面ABCD,EF面ABCD,∴EF⊥AP,在△ABC中,AB=AC,![]() ,
,
在平行四边形![]() 中,得∠ABC=∠ACB=45°,∴AB⊥AC,且
中,得∠ABC=∠ACB=45°,∴AB⊥AC,且![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
∴四边形ABEF为平行四边形,∴AB∥EF,∴AC⊥EF,
∵AP∩AC=C,AP面PAC,AC面PAC,∴EF⊥面PAC.
(2)连接AE,AM,△ABC中,∵AB=AC,E为BC的中点,∴AE⊥BC,平行四边形ABCD中,AD∥BC,∴AE⊥AD,
∵PA⊥平面ABCD,AE平面ABCD,∴AE⊥PA,∵PA∩AD=A,∴AE⊥平面PAD,
∴AM是EM在平面PAD中的射影,∴∠EMA是EM与平面PAD所成的角,
等腰直角三角形ABC,AB=AC=2,∴BC=![]() AB=2
AB=2![]() ,∴AD=2
,∴AD=2![]() ,
,![]() ,
,
∵PA⊥平面ABCD,∴PA⊥AD,∵PA=4,∴PD=![]() ,
,
又M为PD的中点,故![]() ,在Rt△MAE中,tan∠EMA=
,在Rt△MAE中,tan∠EMA=![]() =
=![]() ,
,
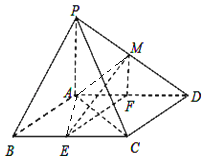
∴直线ME与平面PAD所成角的正切值为![]() ,所以直线
,所以直线![]() 与平面
与平面![]() 所成的角
所成的角![]()


科目:高中数学 来源: 题型:
【题目】已知下列命题:
①在线性回归模型中,相关指数![]() 表示解释变量
表示解释变量![]() 对于预报变量
对于预报变量![]() 的贡献率,
的贡献率, ![]() 越接近于1,表示回归效果越好;
越接近于1,表示回归效果越好;
②两个变量相关性越强,则相关系数的绝对值就越接近于1;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均减少0.5个单位;
平均减少0.5个单位;
④对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值
的观测值![]() 来说,
来说, ![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大.其中正确命题的序号是__________.
有关系”的把握程度越大.其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点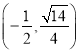 ,且离心率为
,且离心率为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 的右顶点,探究:
的右顶点,探究: ![]() 是否为定值,若是,求出该定值,若不是,请说明理由.(其中,
是否为定值,若是,求出该定值,若不是,请说明理由.(其中, ![]() ,
, ![]() 分别是直线
分别是直线![]() 、
、![]() 的斜率)
的斜率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的反函数为
的反函数为![]() ,若存在函数
,若存在函数![]() 使得对函数
使得对函数![]() 定义域内的任意
定义域内的任意![]() 都有
都有![]() ,则称函数
,则称函数![]() 为函数
为函数![]() 的“Inverse”函数.
的“Inverse”函数.
(1)判断下列哪个函数是函数![]() 的“Inverse”函数并说明理由.
的“Inverse”函数并说明理由.
①![]() ;②
;②![]() ;
;
(2)设函数![]() 存在反函数
存在反函数![]() ,证明函数
,证明函数![]() 存在唯一的“Inverse”函数的充要条件是函数
存在唯一的“Inverse”函数的充要条件是函数![]() 的值域为
的值域为![]() ;
;
(3)设函数![]() 存在反函数
存在反函数![]() ,函数
,函数![]() 为
为![]() 的一个“Inverse”函数,记
的一个“Inverse”函数,记![]() ,其中
,其中![]() ,若对函数
,若对函数![]() 定义域内的任意
定义域内的任意![]() 都有
都有![]() ,求所有满足条件的函数
,求所有满足条件的函数![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义域为
是定义域为![]() 上的函数,若对任意的实数
上的函数,若对任意的实数![]() ,都有:
,都有:![]() 成立,当且仅当
成立,当且仅当![]() 时取等号,则称函数
时取等号,则称函数![]() 是
是![]() 上的凸函数,凸函数具有以下性质:对任意的实数
上的凸函数,凸函数具有以下性质:对任意的实数![]() ,都有:
,都有:![]() 成立,当且仅当
成立,当且仅当![]() 时取等号,设
时取等号,设![]()
(1)求证:![]() 是
是![]() 上的凸函数
上的凸函数
(2)设![]() ,
,![]() ,利用凸函数的定义求
,利用凸函数的定义求![]() 的最大值
的最大值
(3)设![]() 是
是![]() 三个内角,利用凸函数性质证明
三个内角,利用凸函数性质证明![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在实数集![]() 中,定义两个实数
中,定义两个实数![]() 、
、![]() 的运算法则△如下:若
的运算法则△如下:若![]() ,则
,则![]() ,若
,若![]() ,则
,则![]() .
.
(1)请分别计算![]() 和
和![]() 的值;
的值;
(2)对于实数![]() ,判断
,判断![]() 是否恒成立,并说明理由;
是否恒成立,并说明理由;
(3)求函数![]() 的解析式,其中
的解析式,其中![]() ,并求函数的最值.(符号“
,并求函数的最值.(符号“![]() ”表示相乘)
”表示相乘)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台为宣传本省,随机对本省内![]() 岁的人群抽取了n人,回答问题“本省内著名旅游景点有哪些”统计结果如图表所示
岁的人群抽取了n人,回答问题“本省内著名旅游景点有哪些”统计结果如图表所示
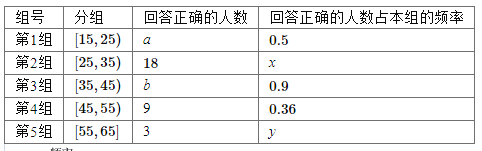
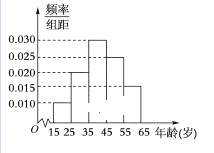
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取6人,求第
组回答正确的人中用分层抽样的方法抽取6人,求第![]() 组每组各抽取多少人?
组每组各抽取多少人?
(3)指出直方图中,这组数据的中位数是多少(取整数值)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】旅行社为某旅行团包飞机去旅游,其中旅行社的包机费为15000元.旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数不超过35人时,飞机票每张收费800元;若旅游团的人数多于35人,则给予优惠,每多1人,机票费每张减少10元,但旅游团的人数最多有60人.设旅行团的人数为![]() 人,飞机票价格为
人,飞机票价格为![]() 元,旅行社的利润为
元,旅行社的利润为![]() 元.
元.
(1)写出飞机票价格![]() 元与旅行团人数
元与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)当旅游团的人数![]() 为多少时,旅行社可获得最大利润?求出最大利润.
为多少时,旅行社可获得最大利润?求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某桶装水经营部每天的房租、人员工资等固定成本为300元,每桶水的进价是8元,销售单价与日均销售量的关系如表所示:
销售单价/元 | 9 | 10 | 11 | 12 | 13 | 14 |
日均销售量/桶 | 550 | 500 | 450 | 400 | 350 | 300 |
请根据以上数据分析,这个店怎样定每桶水的单价才能获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com