已知数列{an}的前n项的和Sn=an-1(a是不为0的实数),那么{an}( )
A.一定是等差数列
B.一定是等比数列
C.或者是等差数列,或者是等比数列
D.既不可能是等差数列,也不可能是等比数列
【答案】
分析:由题意可知,当a=1时,S
n=0,判断数列是否是等差数列;当a≠1时,利用
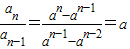
,判断数列{a
n}是等差数列还是等比数列.
解答:解:①当a=1时,S
n=0,
且a
1=a-1=0,
a
n=S
n-S
n-1=(a
n-1)-(a
n-1-1)=0,(n>1)
a
n-1=S
n-1-S
n-2=(a
n-1-1)-(a
n-2-1)=0,
∴a
n-a
n-1=0,
∴数列{a
n}是等差数列.
②当a≠1时,
a
1=a-1,
a
n=S
n-S
n-1=(a
n-1)-(a
n-1-1)=a
n-a
n-1,(n>1)
a
n-1=S
n-1-S
n-2=(a
n-1-1)-(a
n-2-1)=a
n-1-a
n-2,(n>2)
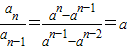
,(n>2)
∴数列{a
n}是等比数列.
综上所述,数列{a
n}或是等差数列或是等比数列.
故选C.
点评:本题考查数列的概念,等差数列与等比数列的判定,解题时要注意a=0的情况,避免丢解以及n的范围满足数列的定义.

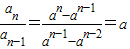 ,判断数列{an}是等差数列还是等比数列.
,判断数列{an}是等差数列还是等比数列.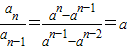 ,(n>2)
,(n>2)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案