
甲乙丙丁4人玩传球游戏,持球者将球等可能的传给其他3人,若球首先从甲传出,经过3次传球.
(1)求球恰好回到甲手中的概率;
(2)设乙获球(获得其他游戏者传的球)的次数为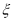 ,求
,求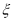 的分布列及数学期望.
的分布列及数学期望.
(1)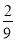 ;(2)分布列详见解析,
;(2)分布列详见解析,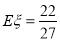 .
.
【解析】
试题分析:本题主要考查古典概型和离散型随机变量的分布列和数学期望等数学知识,考查学生的分析问题解决问题的能力和计算能力.第一问,利用古典概型先求出经过3次传球的传球方法共27种,再求3次传球后,求恰好回到甲手中的种数,相除得到概率值;第二问,先分别求出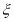 的3种情况的概率,概率的分子可以用树状图数出来,列出分布列,利用
的3种情况的概率,概率的分子可以用树状图数出来,列出分布列,利用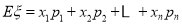 求出数学期望.
求出数学期望.
试题解析:⑴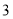 次传球,传球的方法共有
次传球,传球的方法共有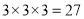 种,
种, 次传球结束时,球恰好回到甲手中的传球方法为
次传球结束时,球恰好回到甲手中的传球方法为 种,故所求概率为
种,故所求概率为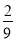 5分
5分
⑵易知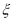 的所有可能取值为
的所有可能取值为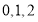 6分
6分
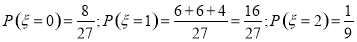 , 9分
, 9分
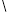
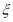 的分布列为
的分布列为
| 0 | 1 | 2 |
|
|
|
|
10分
因此,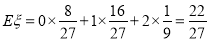 . 12分
. 12分
考点:1.古典概型;2.离散型随机变量的分布列和数学期望.


科目:高中数学 来源:2013-2014学年江西省宜春市高三考前模拟理科数学试卷(解析版) 题型:选择题
已知全集为R,集合M ={xlx2-2x-8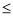 0),集合N={x|(1n2)l-x>1},则集合M
0),集合N={x|(1n2)l-x>1},则集合M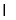 (CRN)等于( )
(CRN)等于( )
A.[-2,1] B.(1,+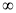 ) C.[-l,4) D.(1,4]
) C.[-l,4) D.(1,4]
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
已知函数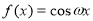
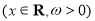 的最小正周期为
的最小正周期为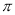 ,为了得到函数
,为了得到函数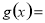
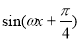 的图象,只要将
的图象,只要将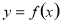 的图象( )
的图象( )
A.向左平移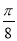 个单位长度 B.向右平移
个单位长度 B.向右平移 个单位长度
个单位长度
C.向左平移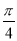 个单位长度 D.向右平移
个单位长度 D.向右平移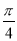 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
已知函数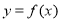 对任意的
对任意的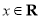 满足
满足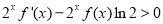 (其中
(其中 是函数
是函数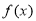 的导函数),则下列不等式成立的是( )
的导函数),则下列不等式成立的是( )
A.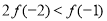 B.
B.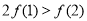 C.
C.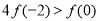 D.
D.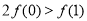
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
复数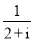 在复平面内对应的点位于( )
在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省高三联合考试理科数学试卷(解析版) 题型:选择题
已知数列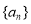 ,若点
,若点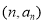
 均在直线
均在直线 上,则数列
上,则数列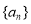 的前9项和
的前9项和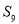 等于( )
等于( )
A.18 B.20 C.22 D.24
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省高三联合考试文科数学试卷(解析版) 题型:选择题
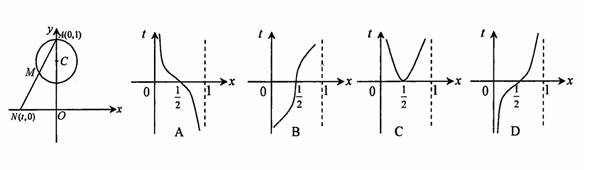
如图,把周长为1的圆的圆心C放在y轴上,顶点A(0,1),一动点M从A开始逆时针绕圆运动一周,记弧AM=x,直线AM与x轴交于点N(t,0),则函数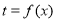 的图像大致为( )
的图像大致为( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com