
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 105 |

 的可靠性要求,能否认为“成绩与班级有关系” .
的可靠性要求,能否认为“成绩与班级有关系” .| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
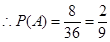 。
。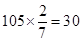 ,非优秀人数为75,可以填完整列联表.
,非优秀人数为75,可以填完整列联表.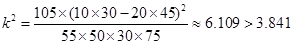 ,从而确定有95%的把握认为“成绩与班级有关系”.
,从而确定有95%的把握认为“成绩与班级有关系”.| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
 …………………5分
…………………5分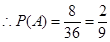 …………………14分
…………………14分

科目:高中数学 来源:不详 题型:解答题
| 月收入(单位百元) | [15,25 | [25,35 | [35,45 | [45,55 | [55,65 | [65,75 |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| | 月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 |
| 赞成 | 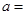 |  | |
| 不赞成 |  |  | |
| 合计 | | | |
 ,求随机变量
,求随机变量 的分布列。
的分布列。

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 得病 | 不得病 | 合计 |
| 干净水 | 52 | 466 | 518 |
| 不干净水 | 94 | 218 | 312 |
| 合计 | 146 | 684 | 830 |
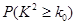 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
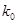 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
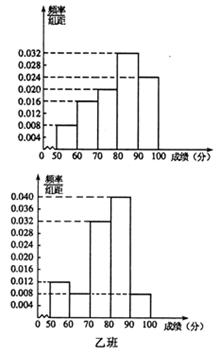
 ,求
,求 的分布列和数学期望;
的分布列和数学期望; 列联表,并判断是否有
列联表,并判断是否有 的把握认为:“成绩优秀”与教学方式有关.
的把握认为:“成绩优秀”与教学方式有关.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 4-4 | 4-5 | 4-7 |
| 男生 | 130 | 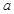 | 80 |
| 女生 |  | 100 | 60 |
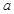 ,
, 的值.
的值.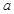 ≥110,
≥110, >110,计算
>110,计算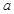 >
> 的概率.
的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
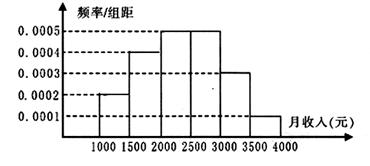
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.(2, 2) | B.(1, 2) | C.(1.5, 0) | D.(1.5 , 5) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的样本,样本中A型号产品有15件,那么样本容量
的样本,样本中A型号产品有15件,那么样本容量 为________
为________查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com