
 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源:不详 题型:解答题
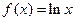 ,
,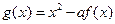 ,
,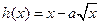 ,已知
,已知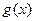 在x=1处取极值.
在x=1处取极值.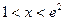 时,恒有
时,恒有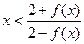 成立;
成立;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
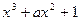 的图象上一点B(1,b)的切线的斜率为-3.
的图象上一点B(1,b)的切线的斜率为-3.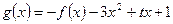 .是否存在一个实数t,使得当
.是否存在一个实数t,使得当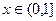 时,g(x)有最大值1?
时,g(x)有最大值1?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
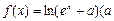 为常数)是实数集R上的奇函数,函数
为常数)是实数集R上的奇函数,函数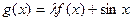 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数. 上恒成立,求
上恒成立,求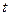 的取值范围;
的取值范围;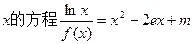 的根的个数.
的根的个数.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 级数 | 全月应纳税所得额 | 税率(﹪) |
| 1 | 小于等于500元 | 5 |
| 2 | 大于500且小于等于2000元 | 10 |
| 3 | 大于2000且小于等于5000元 | 15 |
| A.43元 | B.33元 | C.23元 | D.53元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
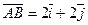 (
(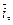
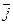 分别是与x轴和y轴正半轴同方向的单位向量),函数g(x)=
分别是与x轴和y轴正半轴同方向的单位向量),函数g(x)=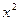 ―x―6,
―x―6,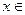 M时,求函数
M时,求函数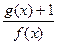 的最小值
的最小值查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
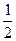 )的值;
)的值;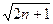 .(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
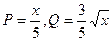 ,今有3万元资金投入经营甲、乙两种商品,为获得最大利润,则对甲、乙两种商品的资金投入分别是多少?能获得最大的利润是多少?
,今有3万元资金投入经营甲、乙两种商品,为获得最大利润,则对甲、乙两种商品的资金投入分别是多少?能获得最大的利润是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com