
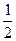 )的值;
)的值;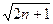 .(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.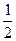 )=-1 (2) 函数y=f(x)在(0,+∞)上是增函数
)=-1 (2) 函数y=f(x)在(0,+∞)上是增函数 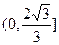
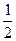 )=f(2)+f(
)=f(2)+f(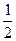 ),且f(2)=1,∴f(
),且f(2)=1,∴f(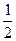 )=-1
)=-1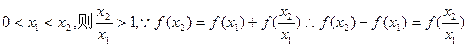 …4分
…4分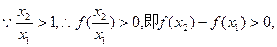
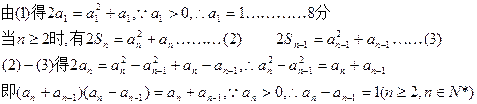
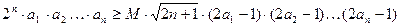
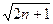 ×1×3×5×…×(2n-1),
×1×3×5×…×(2n-1),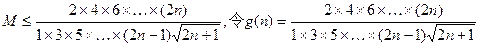
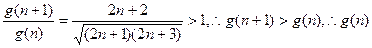 是单调递增
是单调递增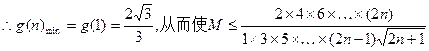 对一切n∈N*都成立的正数M的范围是
对一切n∈N*都成立的正数M的范围是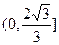


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源:不详 题型:解答题
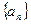 的前
的前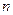 项和
项和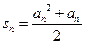 ,
,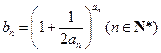 .
.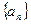 的通项公式;
的通项公式;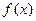 在区间D上是凹函数,且
在区间D上是凹函数,且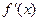 存在,则当
存在,则当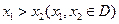 时,总有
时,总有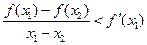 .请根据上述定理,且已知函数
.请根据上述定理,且已知函数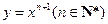 是
是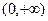 上的凹函数,判断
上的凹函数,判断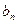 与
与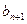 的大小;
的大小;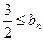 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
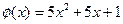
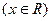 ,函数
,函数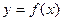 的图象与
的图象与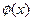 的图象关于点
的图象关于点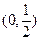 中心对称。
中心对称。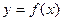 的解析式;
的解析式;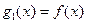 ,
,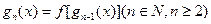 ,试求出使
,试求出使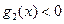 成立的
成立的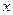 取值范围;
取值范围; ,使
,使 对于区间内的任意实数
对于区间内的任意实数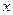 ,只要
,只要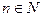 ,且
,且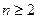 时,都有
时,都有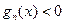 恒成立?
恒成立?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 产品A(件) | 产品B(件) | |
| 研制成本、搭载费用之和(万元) | 20 | 30 | 计划最大资金额300万元 |
| 产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
| 预计收益(万元) | 80 | 60 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com