
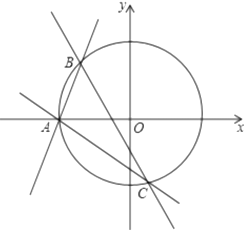
【题目】已知圆 ![]() 与直线
与直线 ![]() 相切.
相切.
(1)求圆 ![]() 的方程;
的方程;
(2)过点 ![]() 的直线
的直线 ![]() 截圆所得弦长为
截圆所得弦长为 ![]() ,求直线
,求直线 ![]() 的方程;
的方程;
(3)设圆 ![]() 与
与 ![]() 轴的负半轴的交点为
轴的负半轴的交点为 ![]() ,过点
,过点 ![]() 作两条斜率分别为
作两条斜率分别为 ![]() 的直线交圆
的直线交圆 ![]() 于
于 ![]() 两点,且
两点,且 ![]() ,证明:直线
,证明:直线 ![]() 恒过一个定点,并求出该定点坐标.
恒过一个定点,并求出该定点坐标.
【答案】
(1)解:
∵圆 ![]() 与直线
与直线 ![]() 相切,
相切,
∴圆心 ![]() 到直线的距离为
到直线的距离为 ![]() ,
,
∴圆 ![]() 的方程为:
的方程为: ![]() .
.
(2)解:若直线 ![]() 的斜率不存在,直线
的斜率不存在,直线 ![]() 为
为 ![]() ,
,
此时直线 ![]() 截圆所得弦长为
截圆所得弦长为 ![]() ,符合题意;
,符合题意;
若直线 ![]() 的斜率存在,设直线
的斜率存在,设直线 ![]() 为
为 ![]() ,即
,即 ![]() ,
,
由题意知,圆心到直线的距离为 ![]() ,解得:
,解得: ![]() ,
,
此时直线 ![]() 为
为 ![]() ,
,
则所求的直线 ![]() 为
为 ![]() 或
或 ![]()
(3)解:由题意知, ![]() ,设直线
,设直线 ![]() ,
,
与圆方程联立得: ![]() ,
,
消去 ![]() 得:
得: ![]() ,
,
∴ ![]()
∴ ![]() ,
, ![]() ,即
,即 ![]() ,
,
∵ ![]() ,用
,用 ![]() 代替
代替 ![]() 得:
得: ![]()
∴直线 ![]() 的方程为:
的方程为: 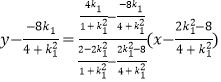
即 ![]()
![]() ,
,
整理得: ![]()
![]()
则直线 ![]() 定点为
定点为 ![]()
【解析】(1)由圆与直线相切得到圆心到切线的距离公式等于圆的半径列出关于r的方程,求出其值即可求出圆的方程。(2)分两种情况:当直线的斜率不存在时直线x=1满足题意;当直线的斜率存在时,设出直线的方程,根据直线与圆的切线得到圆心到直线的距离d=r,列出关于k的方程解出方程求出k的值,进而得到直线的方程,(3)根据题意求出点A的坐标,设出直线AB的方程与圆的方程联立消去y得到关于x的一元二次方程,利用韦达定理表示出两根之积,将A的横坐标代入表示出B的横坐标,进而表示出B的纵坐标确定出B的坐标,由题中 k1 k2 = 2,表示出点C的坐标故可求出直线BC的解析式,进而可得出直线BC恒过一个定点,求出该点坐标即可。
【考点精析】掌握圆的标准方程和直线与圆的三种位置关系是解答本题的根本,需要知道圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.
;圆心为A(a,b),半径为r的圆的方程;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD的底面是菱形,PA⊥面ABCD,PA=AD=2,∠ABC=60°,E为PD中点. 
(1)求证:PB∥平面ACE;
(2)求二面角E﹣AC﹣D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),φ(x)满足关系φ(x)=f(x)f(x+α)(其中α是常数).
(1)如果α=1,f(x)=2x﹣1,求函数φ(x)的值域;
(2)如果α= ![]() ,f(x)=sinx,且对任意x∈R,存在x1 , x2∈R,使得φ(x1)≤φ(x)≤φ(x2)恒成立,求|x1﹣x2|的最小值;
,f(x)=sinx,且对任意x∈R,存在x1 , x2∈R,使得φ(x1)≤φ(x)≤φ(x2)恒成立,求|x1﹣x2|的最小值;
(3)如果f(x)=Asin(ωx+)(A>0,ω>0),求函数φ(x)的最小正周期(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=cos(x+ ![]() )的图象,只需把余弦曲线y=cosx上的所有的点( )
)的图象,只需把余弦曲线y=cosx上的所有的点( )
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若命题p为真命题,命题q为假命题,则命题“p且q”为真命题
B.“ ![]() ”是“
”是“ ![]() ”的充分不必要条件
”的充分不必要条件
C.l为直线,α,β,为两个不同的平面,若l⊥α,α⊥β,则l∥β
D.命题“?x∈R,2x>0”的否定是“?x0∈R, ![]() ≤0”
≤0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P与两定点A(﹣2,0),B(2,0)连线的斜率之积为﹣ ![]() . (Ⅰ)求动点P的轨迹C的方程;
. (Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)若过点F(﹣ ![]() ,0)的直线l与轨迹C交于M、N两点,且轨迹C上存在点E使得四边形OMEN(O为坐标原点)为平行四边形,求直线l的方程.
,0)的直线l与轨迹C交于M、N两点,且轨迹C上存在点E使得四边形OMEN(O为坐标原点)为平行四边形,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆(x﹣1)2+y2= ![]() 于点A,B,C,D四点,则9|AB|+4|CD|的最小值为 .
于点A,B,C,D四点,则9|AB|+4|CD|的最小值为 . 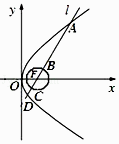
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数称为双曲函数:双曲正弦:shx= ![]() ,双曲余弦:chx=
,双曲余弦:chx= ![]() ,双曲正切:thx=
,双曲正切:thx= ![]() .
.
(1)对比三角函数的性质,请你找出它们的三个类似性质;
(2)求双曲正弦shx的导数,并求在点x=0处的切线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com