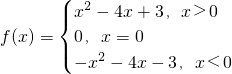Question

已知f（x）是R上的奇函数，且当x∈（-∞，0）时，f（x）=-x²-4x-3，
（1）当x∈（0，+∞）时，f（x）的解析式；
（2）求函数f（x）的零点．

Answer 1

解：（1）当x∈（0，+∞）时，-x∈（-∞，0）
则f（-x）=-（-x）²-4（-x）-3=-x²+4x-3
∵f（x）是R的奇函数∴f（-x）=-f（x）
∴当x∈（0，+∞）时，f（x）=-f（-x）=-[-x²+4x-3]=x²-4x+3
（2）∵f（x）是R的奇函数∴f（0）=0
∴
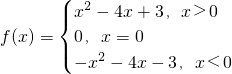
令f（x）=0解得x=0或x=1或x=3或x=-1或x=-3
∴f（x）的零点为0，±1，±3
分析：（1）要求当x∈（0，+∞）的f（x）的解析式而题中给的是当x∈（-∞，0）时f（x）=-x²-4x-3故需将x＞0变形为-x＜0即可代入x∈（-∞，0）时f（x）=-x²-4x-3然后利用奇偶性即可得解．
（2）根据零点的定义令f（x）=0求此方程在各范围内的解即为零点．
点评：本题主要考查了利用函数的奇偶性求函数的解析式进而求函数的零点．第一问解题的关键是将x＞0等价变形为-x＜0然后利用题中的条件和奇偶性即可得解．第二问要求函数的所有零点即要求f（x）（x∈R）的解析式而由题意和（1）可知x＞0，x＜0的解析式而无x=0的解析式因此x=0的解析式的求解就显得非常重要了这是第二问正确解出的关键！