
| A. | 3 | B. | 6 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 利用两角和与差的三角函数化简函数的解析式,通过正弦函数求解最值.
解答 解:f(x)=3sin(x+$\frac{π}{6}$)+$\sqrt{3}$sin($\frac{π}{3}$-x)
=$3(sinxcos\frac{π}{6}+cosxsin\frac{π}{6})$$+\sqrt{3}(sin\frac{π}{3}cosx-cos\frac{π}{3}sinx)$
=$\frac{3\sqrt{3}}{2}sinx+\frac{3}{2}cosx+\frac{3}{2}cosx-\frac{\sqrt{3}}{2}sinx$=$\sqrt{3}sinx+3cosx$
=$2\sqrt{3}(\frac{1}{2}sinx+\frac{\sqrt{3}}{2}cosx)$=$2\sqrt{3}sin(x+\frac{π}{3})$,
又$sin(x+\frac{π}{3})$的最大值是1,
∴函数f(x)=3sin(x+$\frac{π}{6}$)+$\sqrt{3}$sin($\frac{π}{3}$-x)的最大值是$2\sqrt{3}$.
故选:D.
点评 本题考查三角函数的最值的求法,考查计算能力,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
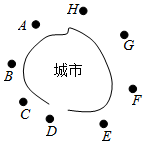 某海滨城市外围有8个小岛,如图,某中学决定分两次去这8个小岛进行社会调查,每次去4个,要求每次至多只能连续两个小岛相邻(如允许ABDE,但不允许ABCE),则能够有30种安排方法.
某海滨城市外围有8个小岛,如图,某中学决定分两次去这8个小岛进行社会调查,每次去4个,要求每次至多只能连续两个小岛相邻(如允许ABDE,但不允许ABCE),则能够有30种安排方法.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 4 | C. | 2或-4 | D. | -2或4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示是一打靶用的靶标,其半径为10cm,被平分成10个同心圆,从里到外各区域分别记在数值10,9,…,2,1,表示打到那个区域就得对应的分值,若某运动员打靶所得分值ξ与打中相应区域的概率P(ξ)的函数关系是P(ξ)=$\frac{1}{55}$(11-ξ).
如图所示是一打靶用的靶标,其半径为10cm,被平分成10个同心圆,从里到外各区域分别记在数值10,9,…,2,1,表示打到那个区域就得对应的分值,若某运动员打靶所得分值ξ与打中相应区域的概率P(ξ)的函数关系是P(ξ)=$\frac{1}{55}$(11-ξ).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com