
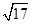 ,求直线l的倾斜角;
,求直线l的倾斜角;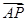 =
=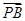 ,求此时直线l的方程.
,求此时直线l的方程.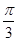 或
或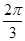 . (2)x-y=0或x+y-2=0.
. (2)x-y=0或x+y-2=0.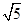 ,
,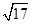 ,故弦心距d=
,故弦心距d=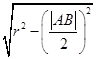 =
=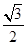 .
. ,
,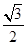 =
= ,解得m=±
,解得m=±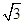 .
.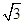 ,故直线l的倾斜角等于
,故直线l的倾斜角等于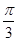 或
或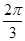 .
.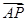 =
=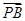 可得2(1-x1,-mx1+m)=(x2-1,mx2-m),
可得2(1-x1,-mx1+m)=(x2-1,mx2-m),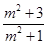 关系可得x1+x2=
关系可得x1+x2=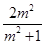 .②
.②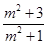 ,故点A的坐标为(
,故点A的坐标为(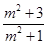 ,
,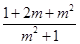 ).
).

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.x+4y-4=0 | B.4x+y-4=0 | C.x-4y+4=0 | D.x-4y-4=0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.m<1 | B.-3<m<1 | C.-4<m<2 | D.0<m<1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
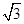 ,则直线l的方程为( )
,则直线l的方程为( )| A.x=-1或4x+3y-4=0 |
| B.x=-1或4x-3y+4=0 |
| C.x=1或4x-3y+4=0 |
| D.x=1或4x+3y-4=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com