
【题目】已知函数f(x)=﹣2sin(2x+φ)(|φ|<π),若 ![]() ,则f(x)的一个单调递增区间可以是( )
,则f(x)的一个单调递增区间可以是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:∵当x= ![]() 时,f(x)=﹣2sin(2x+φ)有最小值为﹣2 ∴x=
时,f(x)=﹣2sin(2x+φ)有最小值为﹣2 ∴x= ![]() 是方程2x+φ=
是方程2x+φ= ![]() +2kπ的一个解,得φ=
+2kπ的一个解,得φ= ![]() +2kπ,(k∈Z)
+2kπ,(k∈Z)
∵|φ|<π,∴取k=0,得φ= ![]() .
.
因此函数表达式为:f(x)=﹣2sin(2x+ ![]() )
)
令 ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,得
+2kπ,得 ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,(k∈Z)
+kπ,(k∈Z)
取k=0,得f(x)的一个单调递增区间是 ![]()
故选:D
由正弦函数最值的结论,得x= ![]() 是方程2x+φ=
是方程2x+φ= ![]() +2kπ的一个解,结合|φ|<π得φ=
+2kπ的一个解,结合|φ|<π得φ= ![]() ,所以f(x)=﹣2sin(2x+
,所以f(x)=﹣2sin(2x+ ![]() ),再根据正弦函数的图象与性质,得函数的单调增区间为[
),再根据正弦函数的图象与性质,得函数的单调增区间为[ ![]() +kπ,
+kπ, ![]() +kπ](k∈Z),对照各选项可得本题答案.
+kπ](k∈Z),对照各选项可得本题答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知甲、乙两个旅游景点之间有一条5km的直线型水路,一艘游轮以![]() 的速度航行时
的速度航行时![]() 考虑到航线安全要求
考虑到航线安全要求![]() ,每小时使用的燃料费用为
,每小时使用的燃料费用为![]() 万元
万元![]() 为常数,且
为常数,且![]() ,其他费用为每小时
,其他费用为每小时![]() 万元.
万元.
![]() 若游轮以
若游轮以![]() 的速度航行时,每小时使用的燃料费用为
的速度航行时,每小时使用的燃料费用为![]() 万元,要使每小时的所有费用不超过
万元,要使每小时的所有费用不超过![]() 万元,求x的取值范围;
万元,求x的取值范围;
![]() 求该游轮单程航行所需总费用的最小值.
求该游轮单程航行所需总费用的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学同学的成绩如表:
n | 1 | 2 | 3 | 4 | 5 |
x0 | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6及这6位同学成绩的标准差s;
(2)若从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间[68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,当点
,当点![]() 在圆上运动时,点
在圆上运动时,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,
两点,![]() 为坐标原点,求
为坐标原点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了2010年亚洲某些国家的国民平均寿命![]() 单位:岁
单位:岁![]() .
.
国家 | 平均寿命 | 国家 | 平均寿命 | 国家 | 平均寿命 |
阿曼 |
| 阿富汗 | 59 | 巴基斯坦 |
|
巴林 | | 阿联酋 |
| 马来西亚 |
|
朝鲜 |
| 东帝汶 |
| 孟加拉国 |
|
韩国 |
| 柬埔寨 |
| 塞浦路斯 |
|
老挝 |
| 卡塔尔 |
| 沙特阿拉伯 |
|
蒙古 |
| 科威特 | | 哈萨克斯坦 |
|
缅甸 |
| 菲律宾 |
| 印度尼西亚 |
|
日本 |
| 黎巴嫩 |
| 土库曼斯坦 | 65 |
泰国 |
| 尼泊尔 | 68 | 吉尔吉斯斯坦 |
|
约旦 |
| 土耳其 |
| 乌兹别克斯坦 |
|
越南 | 75 | 伊拉克 |
| 也门 |
|
中国 |
| 以色列 |
| 文莱 |
|
伊朗 | 74 | 新加坡 |
| 叙利亚 |
|
印度 |
|
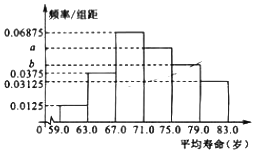
![]() 根据这40个国家的样本数据,得到如图所示的频率分布直方图,其中样本数据的分组区间为:
根据这40个国家的样本数据,得到如图所示的频率分布直方图,其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 请根据上述所提供的数据,求出频率分布直方图中的a,b;
请根据上述所提供的数据,求出频率分布直方图中的a,b;
![]() 请根据统计思想,利用
请根据统计思想,利用![]() 中的频率分布直方图估计亚洲人民的平均寿命及国民寿命的中位数
中的频率分布直方图估计亚洲人民的平均寿命及国民寿命的中位数![]() 保留一位小数
保留一位小数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关线性回归分析的四个命题:
①线性回归直线必过样本数据的中心点(![]() );
);
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数![]() 时,两个变量正相关;
时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数![]() 就越接近于
就越接近于![]() .
.
其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一口袋中装有大小相同的2个白球和4个黑球,每次从袋中任意摸出一个球 .
(1)采取有放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(2)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的均值和方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com