
【题目】一口袋中装有大小相同的2个白球和4个黑球,每次从袋中任意摸出一个球 .
(1)采取有放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(2)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的均值和方差.
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() x2 , g(x)=
x2 , g(x)= ![]() x2+x,m∈R,令F(x)=f(x)+g(x). (Ⅰ)求函数f(x)的单调递增区间;
x2+x,m∈R,令F(x)=f(x)+g(x). (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若关于x的不等式F(x)≤mx﹣1恒成立,求整数m的最小值;
(Ⅲ)若m=﹣1,且正实数x1 , x2满足F(x1)=﹣F(x2),求证:x1+x2 ![]() ﹣1.
﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足 an+2﹣an+1=an+1﹣an , n∈N* , 且a5= ![]() 若函数f(x)=sin2x+2cos2
若函数f(x)=sin2x+2cos2 ![]() ,记yn=f(an),则数列{yn}的前9项和为( )
,记yn=f(an),则数列{yn}的前9项和为( )
A.O
B.﹣9
C.9
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=log2(3-x).
(1)若g(x)=f(2+x)+f(2-x),判断g(x)的奇偶性;
(2)记h(x)是y=f(3-x)的反函数,设A、B、C是函数h(x)图象上三个不同的点,它们的纵坐标依次是m、m+2、m+4且m≥1;试求△ABC面积的取值范围,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,且y与x之间的函数关系式用如图所示的程序框图给出.
(1)写出程序框图中①,②,③处应填充的式子.
(2)若输出的面积y值为6,则路程x的值为多少?
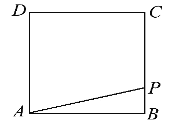

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3+ax2+bx+1的导数![]() 满足
满足![]() ,
,![]() ,其中常数a,b∈R.
,其中常数a,b∈R.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设![]() ,求函数g(x)的极值.
,求函数g(x)的极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com