
| A. | $\frac{9}{2}$ | B. | $\frac{9}{4}$ | C. | 1 | D. | 9 |
分析 由题意可得:可得a+bm+c-2=0.又Q(4,0)到动直线l0的最大距离为3,可得$\sqrt{(4-1)^{2}+{m}^{2}}$=3,解得m=0.a+c=2.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:动直线l0:ax+by+c-2=0(a>0,c>0)恒过点P(1,m),∴a+bm+c-2=0.
又Q(4,0)到动直线l0的最大距离为3,
∴$\sqrt{(4-1)^{2}+{m}^{2}}$=3,解得m=0.
∴a+c=2.
则$\frac{1}{2a}$+$\frac{2}{c}$=$\frac{1}{2}$(a+c)$(\frac{1}{2a}+\frac{2}{c})$=$\frac{1}{2}(\frac{5}{2}+\frac{c}{2a}+\frac{2a}{c})$≥$\frac{1}{2}$$(\frac{5}{2}+2\sqrt{\frac{c}{2a}•\frac{2a}{c}})$=$\frac{9}{4}$,当且仅当c=2a=$\frac{4}{3}$时取等号.
故选:B.
点评 本题考查了直线方程、点到直线的距离公式、两点之间的距离公式、基本不等式的性质,考查了推理能力 与计算能力,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
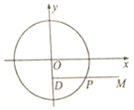 如图,已知DP⊥y轴,点D为垂足,点M在线段DP的延长线上,且满足|DP|=|PM|,当点P在圆x2+y2=3上运动时
如图,已知DP⊥y轴,点D为垂足,点M在线段DP的延长线上,且满足|DP|=|PM|,当点P在圆x2+y2=3上运动时查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{3\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a?α,若b∥a,则b∥α | B. | α⊥β,α∩β=c,b⊥c,则b⊥β | ||
| C. | a⊥b,b⊥c,则a∥c | D. | a∩b=A,a?α,b?α,a∥β,b∥β,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com