
分析 设AB=x,则AC=2x,根据面积公式得S△ABC=$\sqrt{1-co{s}^{2}B}$x,由余弦定理求得 cosC代入化简 S△ABC=$\sqrt{\frac{16}{9}-\frac{9({x}^{2}-\frac{20}{9})^{2}}{16}}$,由三角形三边关系求得$\frac{2}{3}$<x<2,由二次函数的性质求得S△ABC取得最大值.
解答 解:依题意,设AB=x,则AC=2x,又BC=2,
根据面积公式得S△ABC=$\frac{1}{2}$AB•BC•sinB=sinBx=$\sqrt{1-co{s}^{2}B}$x.
由余弦定理得:cosB=$\frac{{x}^{2}+{2}^{2}-(2x)^{2}}{2×2×x}$=$\frac{4-3{x}^{2}}{4x}$,
∴S△ABC=$\sqrt{1-co{s}^{2}B}$x=$\sqrt{1-(\frac{4-3{x}^{2}}{4x})^{2}}$x=$\sqrt{\frac{16}{9}-\frac{9({x}^{2}-\frac{20}{9})^{2}}{16}}$
由三角形三边关系有:x+2x>2且x+2>2x,解得:$\frac{2}{3}$<x<2,
故当 x=$\frac{2\sqrt{5}}{3}$时,S△ABC取得最大值$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题主要考查了余弦定理和面积公式在解三角形中的应用.当涉及最值问题时,可考虑用函数的单调性和定义域等问题,考查了转化思想,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
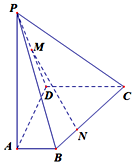 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点M为PD的中点,点N是为棱CB上一点,且$\overrightarrow{BN}=λ\overrightarrow{BC},λ∈({0,1})$.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点M为PD的中点,点N是为棱CB上一点,且$\overrightarrow{BN}=λ\overrightarrow{BC},λ∈({0,1})$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有42株树木的底部周长小于110cm.
为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有42株树木的底部周长小于110cm.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{9}{4}$ | C. | 1 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 144 | B. | 100 | C. | 169 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4\sqrt{2}}{9}$ | B. | -$\frac{2\sqrt{2}}{9}$ | C. | $\frac{2\sqrt{2}}{9}$ | D. | $\frac{4\sqrt{2}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,12) | B. | (2,3) | C. | (2,3] | D. | [-1,12] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com