
| A. | -$\frac{4\sqrt{2}}{9}$ | B. | -$\frac{2\sqrt{2}}{9}$ | C. | $\frac{2\sqrt{2}}{9}$ | D. | $\frac{4\sqrt{2}}{9}$ |
分析 由已知利用诱导公式可求sinα,利用同角三角函数基本关系式可求cosα,进而利用二倍角正弦函数公式即可计算得解.
解答 解:∵sin(π-α)=$\frac{1}{3}$,
∴sinα=$\frac{1}{3}$,
又∵$\frac{π}{2}$≤α≤π,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{2\sqrt{2}}{3}$,
∴sin2α=2sinαcosα=2×$\frac{1}{3}×$(-$\frac{2\sqrt{2}}{3}$)=-$\frac{4\sqrt{2}}{9}$.
故选:A.
点评 本题主要考查了诱导公式,同角三角函数基本关系式,二倍角正弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
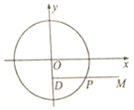 如图,已知DP⊥y轴,点D为垂足,点M在线段DP的延长线上,且满足|DP|=|PM|,当点P在圆x2+y2=3上运动时
如图,已知DP⊥y轴,点D为垂足,点M在线段DP的延长线上,且满足|DP|=|PM|,当点P在圆x2+y2=3上运动时查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a?α,若b∥a,则b∥α | B. | α⊥β,α∩β=c,b⊥c,则b⊥β | ||
| C. | a⊥b,b⊥c,则a∥c | D. | a∩b=A,a?α,b?α,a∥β,b∥β,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 70 | C. | 80 | D. | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com