
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,通过讨论t的范围,求出函数的最小值即可;
(Ⅱ)问题转化为m=lnx+x+$\frac{2}{x}$有两个不同的实数根,令h(x)=lnx+x+$\frac{2}{x}$,(x>0),根据函数的单调性求出h(x)的最小值,求出m的范围,从而判断f(1)+g(1)的符号即可;
(Ⅲ)问题转化为存在x0∈[$\frac{1}{e}$,e]使得m≤${(\frac{2x{-x}^{2}}{lnx-x})}_{max}$成立,令k(x)=$\frac{2x{-x}^{2}}{lnx-x}$,x∈[$\frac{1}{e}$,e],根据函数的单调性求出m的范围即可.
解答 解:(Ⅰ)f′(x)=lnx+1,
令f′(x)>0,解得:x>$\frac{1}{e}$,令f′(x)<0,解得:0<x<$\frac{1}{e}$,
∴f(x)在(0,$\frac{1}{e}$)递减,在($\frac{1}{e}$,+∞)递增,
若t≥$\frac{1}{e}$,则f(x)在[t,t+2]递增,
∴f(x)min=f(t)=tlnt+2,
若0<t<$\frac{1}{e}$,则f(x)在[t,$\frac{1}{e}$)递减,在($\frac{1}{e}$,t+2]递增,
∴f(x)min=f($\frac{1}{e}$)=2-$\frac{1}{e}$;
(Ⅱ)若方程f(x)+g(x)=0有两个不同的实数根,
即m=lnx+x+$\frac{2}{x}$有两个不同的实数根,
令h(x)=lnx+x+$\frac{2}{x}$,(x>0),
即函数y=m和h(x)=lnx+x+$\frac{2}{x}$有两个不同的交点,
而h′(x)=$\frac{1}{x}$+1-$\frac{2}{{x}^{2}}$=$\frac{(x+2)(x-1)}{{x}^{2}}$,
令h′(x)>0,解得:x>1,令h′(x)<0,解得:0<x<1,
故h(x)在(0,1)递减,在(1,+∞)递增,
故h(x)≥h(1)=3,
故m>3,
故f(1)+g(1)=3-m<0;
(Ⅲ)若存在x0∈[$\frac{1}{e}$,e]使得mf′(x)+g(x)≥2x+m成立,
即存在x0∈[$\frac{1}{e}$,e]使得m≤${(\frac{2x{-x}^{2}}{lnx-x})}_{max}$成立,
令k(x)=$\frac{2x{-x}^{2}}{lnx-x}$,x∈[$\frac{1}{e}$,e],则k′(x)=$\frac{(1-x)(2lnx-x)}{{(lnx-x)}^{2}}$,
易得2lnx-x<0,
令k′(x)>0,解得:x>1,令k′(x)<0,解得:x<1,
故k(x)在[$\frac{1}{e}$,1)递减,在(1,e]递增,
故k(x)的最大值是k($\frac{1}{e}$)或k(e),
而k($\frac{1}{e}$)=$\frac{2e-1}{{-e}^{2}-e}$<k(e)=$\frac{2e{-e}^{2}}{1-e}$,
故m≤$\frac{2e{-e}^{2}}{1-e}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查转化思想,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | a≤-1 | B. | a≤2 | C. | a≥-1 | D. | a≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{2}}{3}$ | B. | -$\frac{2\sqrt{2}}{3}$ | C. | -$\frac{4\sqrt{2}}{9}$ | D. | $\frac{4\sqrt{2}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$+1 | C. | $\sqrt{3}$ | D. | $\sqrt{3}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4\sqrt{2}}{9}$ | B. | -$\frac{2\sqrt{2}}{9}$ | C. | $\frac{2\sqrt{2}}{9}$ | D. | $\frac{4\sqrt{2}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}+1$ | B. | $\sqrt{7}+1$ | C. | $\sqrt{2}$-1 | D. | $\sqrt{7}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
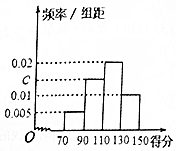 某校为了解校园安全管理专项活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
某校为了解校园安全管理专项活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.| 等级 | 不及格 | 及格 | 良好 | 优秀 |
| 得分 | [70,90) | [90,110) | [110,130) | [130,150] |
| 频数 | 6 | a | 24 | b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com