
分析 利用二项式定理的通项公式求出a,在结合函数的单调性即可求解在区间[-$\frac{2}{3}$,2]上函数f(x)的值域.
解答 解:由题意($\sqrt{x}$-$\frac{a}{{x}^{2}}$)5的常数项为15,即${C}_{5}^{r}(-\frac{a}{{x}^{2}})^{r}({x}^{\frac{1}{2}})^{5-r}$中$-2r+\frac{1}{2}(5-r)=0$,解得:r=1,
则${C}_{5}^{1}(-a)^{1}=15$,可得a=-3.
那么可得函数f(x)=log${\;}_{\frac{1}{3}}$(x+1)+$\frac{3}{x+1}$,
∵在区间[-$\frac{2}{3}$,2]上y=log${\;}_{\frac{1}{3}}$(x+1)和y=$\frac{3}{x+1}$都是减函数,
∴函数f(x)在区间[-$\frac{2}{3}$,2]上是减函数
当x=$-\frac{2}{3}$时,函数f(x)取得最大值为10.
当x=2时,函数f(x)取得最小值为0.
∴函数f(x)=log${\;}_{\frac{1}{3}}$(x+1)+$\frac{3}{x+1}$在区间[-$\frac{2}{3}$,2]上的值域为[0,10]
故答案为:[0,10]
点评 本题考查二项式定理的通项公式和对数函数的单调性的判断以及运用求解值域的问题,属于中档题.


科目:高中数学 来源: 题型:选择题
 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题,松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a=10,b=4,则输出的n=( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题,松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a=10,b=4,则输出的n=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 70 | C. | 80 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
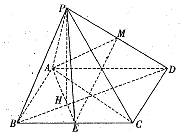 四棱锥P-ABCD中,底面ABCD为矩形,$AB=2,BC=2\sqrt{2},E$为BC的中点,连接AE,BD,交点H,PH⊥平面ABCD,M为PD的中点.
四棱锥P-ABCD中,底面ABCD为矩形,$AB=2,BC=2\sqrt{2},E$为BC的中点,连接AE,BD,交点H,PH⊥平面ABCD,M为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是菱形,$∠DAB=\frac{π}{3}$,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,E是AB中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,$∠DAB=\frac{π}{3}$,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,E是AB中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com