
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 利用诱导公式cos( $\frac{π}{2}$-α)=sinα及余弦函数的单调性和充要条件的定义可得答案.
解答 解:因为cosA<sinB,所以cosA>cos($\frac{π}{2}$-B),
又因为角A,B均为锐角,所以$\frac{π}{2}$-B为锐角,
又因为余弦函数在(0,π)上单调递减,
所以A<$\frac{π}{2}$-B,所以A+B<$\frac{π}{2}$
△ABC中,A+B+C=π,所以C>$\frac{π}{2}$,
所以△ABC为钝角三角形,
若△ABC为钝角三角形,角A、B均为锐角
所以C>$\frac{π}{2}$,
所以A+B<$\frac{π}{2}$
所以A<$\frac{π}{2}$-B,
所以cosA>cos($\frac{π}{2}$-B),
即cosA>sinB
故cosA>sinB是△ABC为钝角三角形的充要条件.
故选:C
点评 本题考查诱导公式及正弦函数的单调性及三角形的基本知识,以及充要条件的定义,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{2}}{3}$ | B. | -$\frac{2\sqrt{2}}{3}$ | C. | -$\frac{4\sqrt{2}}{9}$ | D. | $\frac{4\sqrt{2}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
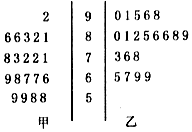 某大学高等数学老师这学期分别用A、B两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图如图:
某大学高等数学老师这学期分别用A、B两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图如图:| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间x | 1 | 1.5 | 2 | 2.5 | 3 |
| 命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
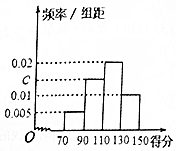 某校为了解校园安全管理专项活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.
某校为了解校园安全管理专项活动的成效,对全校3000名学生进行一次安全意识测试,根据测试成绩评定“优秀”、“良好”、“及格”、“不及格”四个等级,现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下所示.| 等级 | 不及格 | 及格 | 良好 | 优秀 |
| 得分 | [70,90) | [90,110) | [110,130) | [130,150] |
| 频数 | 6 | a | 24 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{π}{2},-\frac{π}{4})$ | B. | $(-\frac{π}{4},\frac{π}{2})$ | C. | $(\frac{π}{2},π)$ | D. | $(\frac{3π}{2},2π)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com