
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,将内层函数看作整体,求出其范围,根据值域是[-$\frac{1}{2}$,$\frac{1}{2}$],建立关系,讨论常数ω所有可能的值.
解答 解:函数f(x)=$\sqrt{3}$sinωxcosωx+cos2ωx,
化简可得:f(x)=$\frac{\sqrt{3}}{2}sin2ωx+\frac{1}{2}cos2ωx+\frac{1}{2}$=sin(2ωx+$\frac{π}{6}$)$+\frac{1}{2}$,
∵x∈[$\frac{π}{6}$,$\frac{π}{3}$],f(x)∈[$-\frac{1}{2}$,$\frac{1}{2}$],
∴-1≤sin(2ωx+$\frac{π}{6}$)≤0,
则$\frac{T}{4}≤\frac{π}{3}-\frac{π}{6}≤\frac{T}{2}$,
而T=$\frac{2π}{2ω}=\frac{π}{ω}$,
那么:$\frac{π}{4ω}≤\frac{π}{6}≤\frac{π}{2ω}$,即$\frac{3}{2}≤ω≤3$.
sin(2ωx+$\frac{π}{6}$)=0的结果必然是$x=\frac{π}{6}$或$\frac{π}{3}$.
当$x=\frac{π}{6}$时,解得ω=$\frac{5}{2}$满足题意.
当x=$\frac{π}{3}$时,解得ω=$\frac{11}{4}$满足题意.
∴常数ω所有可能的值的个数为2.
故选C:
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
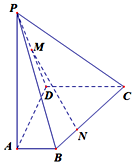 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点M为PD的中点,点N是为棱CB上一点,且$\overrightarrow{BN}=λ\overrightarrow{BC},λ∈({0,1})$.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点M为PD的中点,点N是为棱CB上一点,且$\overrightarrow{BN}=λ\overrightarrow{BC},λ∈({0,1})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤-1 | B. | a≤2 | C. | a≥-1 | D. | a≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 60 | C. | 120 | D. | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4\sqrt{2}}{9}$ | B. | -$\frac{2\sqrt{2}}{9}$ | C. | $\frac{2\sqrt{2}}{9}$ | D. | $\frac{4\sqrt{2}}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com