练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．执行如图所示的程序框图，则输出S的值是（　　）
    A．9B．16C．25D．27

    分析 按照程序的流程，写出前几次循环的结果，并同时判断各个结果是否满足判断框中的条件，直到满足条件，执行输出即可得解．

    解答 解：模拟程序的运行，可得
    S=0，i=1
    执行循环体，S=1，i=3
    不满足条件i＞7，执行循环体，S=4，i=5
    不满足条件i＞7，执行循环体，S=9，i=7
    不满足条件i＞7，执行循环体，S=16，i=9
    满足条件i＞7，退出循环，输出S的值为16．
    故选：B．

    点评 本题主要考查了程序框图的应用，解决程序框图中的循环结构时常采用写出前几次循环的结果，找规律，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．已知数列{an}的前n项和为Sn，且Sn+2=2an•等差数列{bn}的前n项和为Tn，且T2=S2=b3•
    （I）求数列{bn}的通项公式；
    （Ⅱ）令${c_n}={（-1）^n}\frac{{4{T_n}-1}}{b_n^2-1}$，求数列{cn}的前2n项和R2n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知集合A={x||x+1|≥1}，B={x|x≥-1}，则（∁RA）∩B=（　　）
    A．[-1，0]B．[-1，0）C．（-2，-1）D．（-2，-1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知 x＞1，y＞1，且 lg x，2，lg y 成等差数列，则 x+y 有（　　）
    A．最小值 20B．最小值 200C．最大值 20D．最大值 200

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

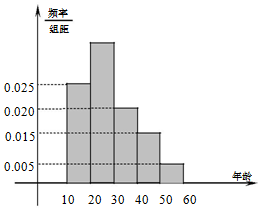    14．•滑雪场开业当天共有 500 人滑雪，滑雪服务中心根据他们的年龄分成[10，20），[20，30），[30，40），[40，50），[50，60]五个组，现按照分层抽样的方法选取 20 人参加有奖活动，这些人的样本数据的频率分布直方图如下图所示，从左往右分别为一组、二组、三组、四组、五组．
    （Ⅰ）求开业当天所有滑雪的人年龄在[20，30）有多少人？
    （Ⅱ）在选取的这 20 人样本中，从年龄不低于 30 岁的人中任选两人参加抽奖活动，求这两个人来自同一组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知函数f（x）=log2（x2-2x-3），则f（x）的定义域为{x|x＞3或x＜-1}，它的单调递增区间是（3，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．设命题p：实数k满足：方程$\frac{{x}^{2}}{k-1}$+$\frac{{y}^{2}}{7-a}$=1表示焦点在y轴上的椭圆；
    命题q，实数k满足：方程（4-k）x2+（k-2）y2=1不表示双曲线．
    （1）若命题q为真命题，求k的取值范围；
    （2）若p是q的必要不充分条件，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．函数f（x）=$\sqrt{3}$sinωxcosωx+cos2ωx（ω＞0）（ω＞0）在区间[$\frac{π}{6}$，$\frac{π}{3}$]的值域是[-$\frac{1}{2}$，$\frac{1}{2}$]，则常数ω所有可能的值的个数是（　　）
    A．0B．1C．2D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

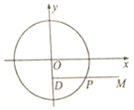    7．如图，已知DP⊥y轴，点D为垂足，点M在线段DP的延长线上，且满足|DP|=|PM|，当点P在圆x2+y2=3上运动时
    （1）求点M的轨迹C的方程；
    （2）直线l：x=my+3（m≠0）交曲线C于A、B两点，设点B关于x轴的对称点为B1（点B1与点A不重合），且直线B1A与x轴交于点E．
    ①证明：点E是定点；
    ②△EAB的面积是否存在最大值？若存在，求出最大值，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案