
【题目】已知函数![]() .
.
(1)若a=0时,求函数![]() 的零点;
的零点;
(2)若a=4时,求函数![]() 在区间[2,5]上的最大值和最小值;
在区间[2,5]上的最大值和最小值;
(3)当![]() 时,不等式
时,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】(1)x=1 (2) 函数![]() 的最大值为12,最小值为5. (3)
的最大值为12,最小值为5. (3) ![]()
【解析】
(1)当![]() 时,去绝对值变分段函数,再求
时,去绝对值变分段函数,再求![]() 的根,即为函数零点;(2)当
的根,即为函数零点;(2)当![]() 时,
时,![]() ;再对
;再对![]() 的取值进行分类讨论去掉绝对值符号:①当
的取值进行分类讨论去掉绝对值符号:①当![]() 时,②当
时,②当![]() 时,分别求出在各自区间上的最值,最后综合得到函数
时,分别求出在各自区间上的最值,最后综合得到函数![]() 的最值;(3)将已知条件等价转化为
的最值;(3)将已知条件等价转化为![]() 恒成立,下面只要利用分离参数法求出函数
恒成立,下面只要利用分离参数法求出函数![]() 和
和![]() 在给定区间上的最值即得.
在给定区间上的最值即得.
(1)当![]() 时,
时,![]()
由![]() 得x=1或x=-3(舍),
得x=1或x=-3(舍),
由![]() 得方程无解,
得方程无解,
综上得,函数![]() 的零点为x=1;
的零点为x=1;
(2)当![]() 时,
时,![]() ;
;
①当![]() 时,
时,![]() ,
,
当x=2时,![]() ;当x=3时,
;当x=3时,![]() ;
;
②当4≤x≤5时,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
综上可知:函数![]() 的最大值为12,最小值为5.
的最大值为12,最小值为5.
(3)若![]() ,原不等式化为
,原不等式化为![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() ,即
,即![]() ,
,
若![]() ,原不等式化为
,原不等式化为![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() ,即
,即![]() ,
,
综上可知:a的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
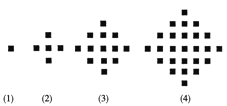
(1) 求出![]() ,
,![]() ,
,![]() 并猜测
并猜测![]() 的表达式;
的表达式;
(2) 求证:![]() +
+![]() +
+![]() +…+
+…+![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年被称为“新高考元年”,随着上海、浙江两地顺利实施“语数外+3”新高考方案,新一轮的高考改革还将继续在全国推进。辽宁地区也将于2020年开启新高考模式,今年秋季入学 的高一新生将面临从物理、化学、生物、政治、历史、地理等6科中任选三科(共20种选法)作为 自己将来高考“语数外+3 ”新高考方案中的“3”。某地区为了顺利迎接新高考改革,在某学校理科班的200名学生中进行了“学生模拟选科数据”调查,每个学生只能从表格中的20种课程 组合选择一种学习。模拟选课数据统计如下表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
组合学科 | 物化生 | 物化政 | 物化历 | 物化地 | 物生政 | 物生历 | 物生地 |
人数 | 20人 | 5人 | 10人 | 10人 | 10人 | 15人 | 10人 |
序号 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
组合学科 | 物政历 | 物政地 | 物历地 | 化生政 | 化生历 | 化生地 | 化政历 |
人数 | 5人 | 0人 | 5人 | ... | 40人 | ... | ... |
序号 | 15 | 16 | 17 | 18 | 19 | 20 | |
组合学科 | 化政地 | 化历地 | 生政历 | 生政地 | 生历地 | 政历地 | 总计 |
人数 | ... | ... | ... | ... | ... | ... | 200人 |
为了解学生成绩与学生模拟选课情之间的关系,用分层抽样的方法从这200名学生中抽取40人的样本进行分析.
(1)样本中选择组合12号“化生历”的有多少人?样本中选择学习物理的有多少人?
(2)从样本选择学习地理且学习物理的学生中随机抽取3人,求这3人中至少有1人还要学习生物的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,曲线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的有( )个
(1). 残差图中残差点所在的水平带状区域越宽,则回归方程的预报精确度越高.
(2). 回归直线一定过样本中心![]() 。
。
(3). 两个模型中残差平方和越小的模型拟合的效果越好。
(4) .甲、乙两个模型的![]() 分别约为0.88和0.80,则模型乙的拟合效果更好.
分别约为0.88和0.80,则模型乙的拟合效果更好.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与正切函数
与正切函数![]() 相邻两支曲线的交点的横坐标分别为
相邻两支曲线的交点的横坐标分别为![]() ,
, ![]() ,且有
,且有![]() ,假设函数
,假设函数![]() 的两个不同的零点分别为
的两个不同的零点分别为![]() ,
, ![]() ,若在区间
,若在区间![]() 内存在两个不同的实数
内存在两个不同的实数![]() ,
, ![]() ,与
,与![]() ,
, ![]() 调整顺序后,构成等差数列,则
调整顺序后,构成等差数列,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() 或不存在 D.
或不存在 D. ![]() 或
或![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(Ⅱ)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,![]() ,∠ABC=∠BCD=90°,E为PB的中点。
,∠ABC=∠BCD=90°,E为PB的中点。

(1)证明:CE∥面PAD.
(2)若直线CE与底面ABCD所成的角为45°,求四棱锥P-ABCD的体积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com