
 B.
B.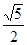 C.
C. D.
D.
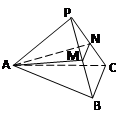
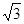 ,设O为底面△ABC中心,连接OB,则∠PBO为三棱锥的侧棱PB与底面所成角,在△POB中求出 tan∠PBO.
,设O为底面△ABC中心,连接OB,则∠PBO为三棱锥的侧棱PB与底面所成角,在△POB中求出 tan∠PBO.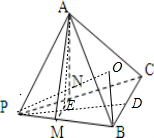 如图,设D为BC中点,则 PD⊥BC,PD⊥MN,垂足为E,E为MN中点.又面AMN⊥面PBC,则 PE⊥面AMN,PE⊥AE.
如图,设D为BC中点,则 PD⊥BC,PD⊥MN,垂足为E,E为MN中点.又面AMN⊥面PBC,则 PE⊥面AMN,PE⊥AE.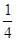 PD2=
PD2=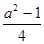 ,ME=
,ME=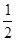 MN=
MN=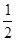 .
.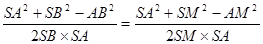 ,代入数据化简得
,代入数据化简得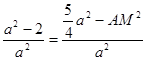 ,AM2=
,AM2=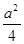 +2,
+2,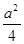 +2-
+2-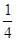 +
+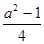 ,解得a2=3,a=
,解得a2=3,a=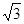 ,设O为底面△ABC中心,连接OB,则∠PBO为三棱锥的侧棱PB与底面所成角,在△POB中,BO=
,设O为底面△ABC中心,连接OB,则∠PBO为三棱锥的侧棱PB与底面所成角,在△POB中,BO=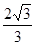 ,由勾股定理,PO2=PB2-BO2=
,由勾股定理,PO2=PB2-BO2=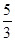 ,PO=
,PO=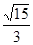 ,所以tan∠PBO=
,所以tan∠PBO=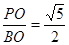 ,
,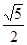 .
.

 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源:不详 题型:单选题
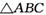 的外接圆为球O的小圆
的外接圆为球O的小圆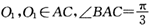 ,AB=1,PA=2.则下列结论正确的是
,AB=1,PA=2.则下列结论正确的是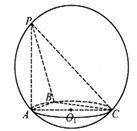

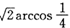
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
, 与底面成30°角。
与底面成30°角。 为垂足,求证:
为垂足,求证: ;
;
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,AD=1,在DC上截取DE=1,将△ADE沿AE
,AD=1,在DC上截取DE=1,将△ADE沿AE
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 C.30° D.90°
C.30° D.90°查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com