
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
(3)当a=1时,求f(|x|)的单调区间.
(1) f(x)的最小值是-1, f(x)的最大值是35. (2) a≤-6或a≥4. (3) f(|x|)的单调递增区间是(0,6],单调递减区间是[-6,0].
解析试题分析:(1)当a=-2时,f(x)=x2-4x+3=(x-2)2-1,
由于x∈[-4,6],
∴f(x)在[-4,2]上单调递减,在[2,6]上单调递增, 2分
∴f(x)的最小值是f(2)=-1, 3分
又f(-4)=35,f(6)=15,故f(x)的最大值是35. 4分
(2)由于函数f(x)的图象开口向上,对称轴是x=-a,
所以要使f(x)在[-4,6]上是单调函数,
应有-a≤-4或-a≥6,即a≤-6或a≥4. 6分
(3)当a=1时,f(x)=x2+2x+3,
∴f(|x|)=x2+2|x|+3,此时定义域为x∈[-6,6], 8分
且f(x)=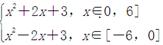 , 10分
, 10分
∴f(|x|)的单调递增区间是(0,6],单调递减区间是[-6,0]. 12分
考点:本题考查了函数的单调性及最值
点评:一元二次函数的单调性与其对称轴有关,故一元二次函数的最值问题往往利用其单调性求解


 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:解答题
对于定义在实数集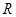 上的两个函数
上的两个函数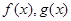 ,若存在一次函数
,若存在一次函数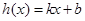 使得,对任意的
使得,对任意的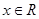 ,都有
,都有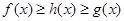 ,则把函数
,则把函数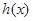 的图像叫函数
的图像叫函数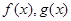 的“分界线”。现已知
的“分界线”。现已知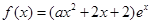 (
(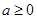 ,
,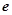 为自然对数的底数),
为自然对数的底数),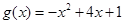
(1)求 的递增区间;
的递增区间;
(2)当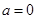 时,函数
时,函数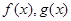 是否存在过点
是否存在过点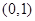 的“分界线”?若存在,求出函数
的“分界线”?若存在,求出函数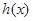 的解析式,若不存在,请说明理由。
的解析式,若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com