
分析 ①由面面平行则法向量共线,反之亦然判断;②由面面垂直的定义判断;③由线在垂直的性持定理判断;④由面面垂直的定义判断.
解答 解:①中平面α,β是指不重合两平面,由$\overrightarrow{n_1}$∥$\overrightarrow{n_2}$⇒α∥β,由α∥β⇒$\overrightarrow{n_1}$∥$\overrightarrow{n_2}$,正确;
②α⊥β,则α与β成90°角,由圆的内接四边形对顶角互补知法向量垂直,反之当法向量垂直,则成90°,由内接四边形对顶角互补,知两平面垂直.正确;
③a与α共面,则a在平面内或与平面平行,∴平面的法向量与直线a垂直,正确;
④若两个平面的法向量不垂直,则成角不是90°,则由圆内角四边形对顶角互补知两平面所成的角不是90°,正确.
∴正确命题的序号实数①②③④.
故答案为:①②③④.
点评 本题主要考查用向量法来解决面面平行,面面垂直等问题,是中档题.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ②④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“如果p2+q2=2,则p+q≤2”的否命题是“如果p+q>2,则p2+q2≠2” | |
| B. | 命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,则p∨q为假 | |
| C. | 若($\sqrt{x}$-$\frac{1}{2\root{3}{x}}$)n的展开式中第四项为常数项,则n=5 | |
| D. | “若am2<bm2,则a<b”的逆命题为真命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a1+a2>0,则a1+a3>0 | B. | 若a1+a3>0,则a1+a2>0 | ||
| C. | 若a1>0,则S2017>0 | D. | 若a1>0,则S2016>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
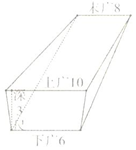 《九章算术》是东方数学思想之源,在卷五《商功》中有以下问题:今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?译文:如图所示的几何体是三个侧面皆为等腰梯形,其他两面为直角三角形的五面体,(前端)下宽6尺,上宽一丈,深3尺,末端宽8尺,无深,长7尺,则它的体积是84立方尺.
《九章算术》是东方数学思想之源,在卷五《商功》中有以下问题:今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺,问积几何?译文:如图所示的几何体是三个侧面皆为等腰梯形,其他两面为直角三角形的五面体,(前端)下宽6尺,上宽一丈,深3尺,末端宽8尺,无深,长7尺,则它的体积是84立方尺.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com