
| A. | ②④ | B. | ①③ | C. | ②③④ | D. | ①②③④⑤ |
分析 设与直线y=x平行的直线方程为:y=x+m,根据对称性不妨取m>0.假设此两条直线的距离d=$\frac{m}{\sqrt{2}}$=$\frac{\sqrt{3}}{2}$t,可得m=$\frac{\sqrt{6}}{2}$t>0,把直线方程y=x+m,代入椭圆方程可得:8x2+6$\sqrt{6}$tx+9t2-6=0,由△≥0,解出即可判断出结论.
解答 解:设与直线y=x平行的直线方程为:y=x+m,根据对称性不妨取m>0.
假设此两条直线的距离d=$\frac{m}{\sqrt{2}}$=$\frac{\sqrt{3}}{2}$t,可得m=$\frac{\sqrt{6}}{2}$t>0,
联立$\left\{\begin{array}{l}{y=x+\frac{\sqrt{6}}{2}t}\\{\frac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$,化为:8x2+6$\sqrt{6}$tx+9t2-6=0,
由△=$(6\sqrt{6}t)^{2}$-32(9t2-6)≥0,
解得:0<$t≤\frac{2\sqrt{6}}{3}$,
因此当0<$t≤\frac{2\sqrt{6}}{3}$时,可知:椭圆上一定存在两个或四个点P满足:使得△MNP为正三角.
故只有②④正确.
故选:A.
点评 本题考查了同样的标准方程及其性质、相互平行的直线斜率之间的关系及其距离、不等式的解法、一元二次方程的解与判别式的关系,考查了推理能力与计算能力,属于中档题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 2n+1-2 | B. | 2n-1 | C. | n2 | D. | n2-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 级数 | 全月应纳税所得额 | 税率(%) |
| 1 | 不超过1500元 | 3 |
| 2 | 1500元-4500元 | 10 |
| A. | 7000元 | B. | 7500元 | C. | 6600元 | D. | 5950元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
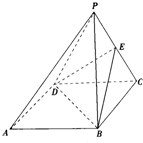 已知四棱锥P-ABCD中,底面四边形为正方形,侧面PDC为正三角形,且平面PDC⊥底面ABCD,E为PC的中点
已知四棱锥P-ABCD中,底面四边形为正方形,侧面PDC为正三角形,且平面PDC⊥底面ABCD,E为PC的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com