
| A. | 2n+1-2 | B. | 2n-1 | C. | n2 | D. | n2-1 |
分析 作出函数f(x)=$\left\{\begin{array}{l}{1-|x-1|,x<2}\\{2f(x-2),x≥2}\end{array}\right.$的图象,可得数列{f(x)}从小到大依次为1,2,4,…,组成以1为首项,2为公比的等比数列,即可求出数列{f(x)}的前n项和.
解答 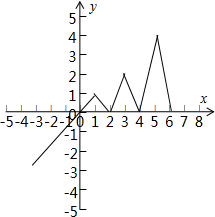 解:函数f(x)=$\left\{\begin{array}{l}{1-|x-1|,x<2}\\{2f(x-2),x≥2}\end{array}\right.$的图象如图所示,
解:函数f(x)=$\left\{\begin{array}{l}{1-|x-1|,x<2}\\{2f(x-2),x≥2}\end{array}\right.$的图象如图所示,
x=1时,f(x)=1,
x=3时,f(x)=2,
x=5时,f(x)=4,
…
所以方程f(x)=g(x)=2${\;}^{\frac{x-1}{2}}$的根从小到大依次为1,3,5,…,数列{f(xn)}从小到大依次为1,2,4,…,组成以1为首项,2为公比的等比数列,
所以数列{f(xn)}的前n项和为$\frac{1-{2}^{n}}{1-2}$=2n-1,
故选:B.
点评 本题考查方程根,考查数列的求和,考查学生分析解决问题的能力,正确作图,确定数列{f(x)}从小到大依次为1,2,4,…,组成以1为首项,2为公比的等比数列是关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-3,-2} | C. | {-3,2} | D. | {-3,-2,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在x=e处取得极小值 | B. | 在x=e处取得极大值 | ||
| C. | 在x=$\frac{1}{e}$处取得极小值 | D. | 在x=$\frac{1}{e}$处取得极大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2] | C. | (-∞,1] | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{25}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
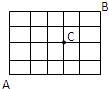 某城市的交通道路如图,从城市的东南角A到城市的西北角B,不经过十字道路维修处C,最近的走法种数有( )
某城市的交通道路如图,从城市的东南角A到城市的西北角B,不经过十字道路维修处C,最近的走法种数有( )| A. | 33 | B. | 60 | C. | 66 | D. | 126 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②④ | B. | ①③ | C. | ②③④ | D. | ①②③④⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com