练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
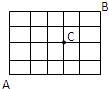
    18．某城市的交通道路如图，从城市的东南角A到城市的西北角B，不经过十字道路维修处C，最近的走法种数有（　　）
    A．33B．60C．66D．126

    分析 先求出从城市的东南角A到城市的西北角B，最近的走法种数，然后求出从城市的东南角A到城市的西北角B，经过十字道路维修处C，最近的走法种数，即可求出从城市的东南角A到城市的西北角B，不经过十字道路维修处C，最近的走法种数．

    解答 解：从城市的东南角A到城市的西北角B，最近的走法种数共有：C94=126种走法．
    从城市的东南角A经过十字道路维修处C，最近的走法有C52=10，从C到城市的西北角B，最近的走法种数C42=6，所以从城市的东南角A到城市的西北角B，经过十字道路维修处C，最近的走法种数：10×6=60．
    所以从城市的东南角A到城市的西北角B，不经过十字道路维修处C，
    最近的走法种数有：126-60=66．
    故选：C．

    点评 本题是中档题，考查排列组合以及简单的计数原理的应用，采用逆向思维是解决本题的关键，考查逻辑思维能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知数列an=1+$\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{n}$（n∈N*）
    求证：a${\;}_{n}^{2}$+$\frac{7}{4}＞$2（a1$+\frac{{a}_{2}}{2}$$+\frac{{a}_{3}}{3}$$+…+\frac{{a}_{n}}{n}$）（n∈N*）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知函数f（x）=$\left\{\begin{array}{l}{1-|x-1|，x＜2}\\{2f（x-2），x≥2}\end{array}\right.$，g（x）=2${\;}^{\frac{x-1}{2}}$，设方程f（x）=g（x）的根从小到大依次为x1，x2…xn…，n∈N+，则数列{f（xn）}的前n项和为（　　）
    A．2n+1-2B．2n-1C．n2D．n2-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．（I）求证：$\sqrt{5}$+$\sqrt{7}$＜2$\sqrt{6}$；
    （Ⅱ）已知a＞0，b＞0且a+b＞2，求证：$\frac{1+a}{b}$，$\frac{1+b}{a}$中至少有一个小于2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．有一圆心角为60°半径为1的扇形铁板．工人师傅要裁出一个面积最大的矩形，下列两种裁法哪一种更好，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在一个口袋里装有4个红球，6个白球，每次从口袋中任意取出一球，记下颜色后再放回口袋内，这样连续取了4次，恰有2次是红球的概率是（　　）
    A．0.3456B．0.3546C．0.375 6D．0.457 6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．函数f（x）=sin（x+$\frac{π}{6}$）+cos2$\frac{x}{2}$的振幅为$\frac{\sqrt{7}}{2}$，最小正周期为2π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=$\frac{A}{2}-\frac{A}{2}$cos2（ωx+φ），（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的图象过点（1，2），相邻两条对称轴间的距离为2，且f（x）的最大值为2．
    （1）求φ；
    （2）计算f（1）+f（2）+…+f（2016）；
    （3）若函数g（x）=f（x）-m-1在区间[1，4]上恰有一个零点，求m的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

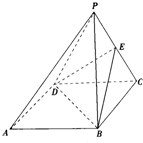    8．已知四棱锥P-ABCD中，底面四边形为正方形，侧面PDC为正三角形，且平面PDC⊥底面ABCD，E为PC的中点
    （1）求证：PA∥平面EDB；
    （2）求证：DE⊥平面PBC．

    查看答案和解析>>

    同步练习册答案