
分析 (I)直接法不易求证,可用分析法进行证明.
(Ⅱ)利用了反证法,假设:$\frac{1+a}{b}$,$\frac{1+b}{a}$都不小于2,则$\frac{1+a}{b}$≥2,$\frac{1+b}{a}$≥2,推得即a+b≤2,这与已知a+b>2矛盾,故假设不成立,从而原结论成立.
解答 证明:(Ⅰ)因为$\sqrt{5}$+$\sqrt{7}$和2$\sqrt{6}$都是正数,所以为了证明$\sqrt{5}$+$\sqrt{7}$<2$\sqrt{6}$,
只要证 ($\sqrt{5}$+$\sqrt{7}$)<(2$\sqrt{6}$),
只需证:12+2$\sqrt{35}$<24,
即证:$\sqrt{35}$<6,
即证:35<36,
因为35<36显然成立,所以原不等式成立.-------(6分)
(Ⅱ)假设$\frac{1+a}{b}$,$\frac{1+b}{a}$都不小于2,则$\frac{1+a}{b}$≥2,$\frac{1+b}{a}$≥2
∵a>0,b>0,∴1+b≥2a,1+a≥2b,
∴1+1+a+b≥2(a+b),即a+b≤2
这与已知a+b>2矛盾,故假设不成立,从而原结论成立.-------------(12分)
点评 本题主要考查了推理论证的两种方法分析法和反证法,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
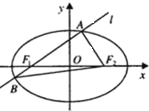 如图,椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$的左、右焦点分别为F1、F2,一条直线l经过F1与椭圆交于A,B两点,若直线l的倾斜角为45°,求△ABF2的面积.
如图,椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$的左、右焦点分别为F1、F2,一条直线l经过F1与椭圆交于A,B两点,若直线l的倾斜角为45°,求△ABF2的面积.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{25}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
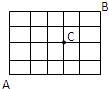 某城市的交通道路如图,从城市的东南角A到城市的西北角B,不经过十字道路维修处C,最近的走法种数有( )
某城市的交通道路如图,从城市的东南角A到城市的西北角B,不经过十字道路维修处C,最近的走法种数有( )| A. | 33 | B. | 60 | C. | 66 | D. | 126 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
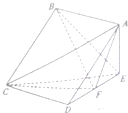 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com