
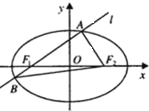
 如图,椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$的左、右焦点分别为F1、F2,一条直线l经过F1与椭圆交于A,B两点,若直线l的倾斜角为45°,求△ABF2的面积.
如图,椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$的左、右焦点分别为F1、F2,一条直线l经过F1与椭圆交于A,B两点,若直线l的倾斜角为45°,求△ABF2的面积. 分析 求出直线l的方程,与椭圆方程联立,消去x,由根与系数的关系求出|y1-y2|的值,即可计算△ABF2的面积S.
解答 解:椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$的左、右焦点分别为F1(-$\sqrt{7}$,0),F2($\sqrt{7}$,0),
直线l的倾斜角为45°,直线的斜率是k=tan45°=1,且过焦点F1(-$\sqrt{7}$,0);
∴直线方程为y=x+$\sqrt{7}$;
∴$\left\{\begin{array}{l}{y=x+\sqrt{7}}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}=1}\end{array}\right.$,
消去x,得9(y-$\sqrt{7}$)2+16y2=144,
整理得25y2-18$\sqrt{7}$y-81=0,y1+y2=$\frac{18\sqrt{7}}{25}$,y1y2=$\frac{-81}{25}$;
∴|y1-y2|=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{(\frac{18\sqrt{7}}{25})^{2}+4×\frac{81}{25}}$=$\frac{72\sqrt{2}}{25}$;
∴△ABF2的面积S=$\frac{1}{2}$|F1F2|•|y1-y2|=$\frac{1}{2}$×2$\sqrt{7}$×$\frac{72\sqrt{2}}{25}$=$\frac{72\sqrt{14}}{25}$.
点评 本题考查了直线与椭圆的方程的应用问题,也考查了椭圆的定义的应用问题,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | y=cos(2x+$\frac{π}{12}$) | B. | y=cos(2x+$\frac{π}{3}$) | C. | y=cos(2x-$\frac{2π}{3}$) | D. | y=cos(2x-$\frac{5π}{12}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | 10 | C. | 20 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
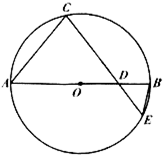 如图,AB是圆O的直径,弦CE交AB于D,CD=4$\sqrt{2}$,DE=$\sqrt{2}$,BD=2.
如图,AB是圆O的直径,弦CE交AB于D,CD=4$\sqrt{2}$,DE=$\sqrt{2}$,BD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$或-1 | D. | -$\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com