
| A. | y=cos(2x+$\frac{π}{12}$) | B. | y=cos(2x+$\frac{π}{3}$) | C. | y=cos(2x-$\frac{2π}{3}$) | D. | y=cos(2x-$\frac{5π}{12}$) |
分析 先求值函数的周期,根据函数图象的平移变换法则,我们可以得到将函数y=cos(2x-$\frac{π}{6}$)的图象向左平移$\frac{1}{4}$个周期后,所得图象对应的解析式.
解答 解:∵y=cos(2x-$\frac{π}{6}$)的周期T=$\frac{2π}{2}$=π,
∴将函数y=cos(2x-$\frac{π}{6}$)的图象向左平移$\frac{1}{4}$个周期后,所得图象对应的解析式为:
y=cos[2(x+$\frac{π}{4}$)-$\frac{π}{6}$]=cos(2x+$\frac{π}{3}$).
故选:B.
点评 本题考查的知识点是函数y=Asin(ωx+φ)的图象变换,其中根据函数图象的平移变换法则--“左加右减”来确定平移前后,函数解析式的关系是解答本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-2,-1)∪(1,2) | C. | (-1,3) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
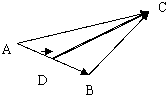 具有方向的线段叫做有向线段(向量),以A为起点,B为终点的有向线段记作$\overrightarrow{AB}$,已知$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$,如图所示:如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{AC}$=$\overrightarrow{a}$+$\overrightarrow{b}$.若D为AB的中点,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$,若BE为AC上的中线,则用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{DC}$为$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
具有方向的线段叫做有向线段(向量),以A为起点,B为终点的有向线段记作$\overrightarrow{AB}$,已知$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$,如图所示:如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{AC}$=$\overrightarrow{a}$+$\overrightarrow{b}$.若D为AB的中点,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$,若BE为AC上的中线,则用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{DC}$为$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 姓名/成绩 | 1 | 2 | 3 | 4 | 5 | 6 |
| 甲 | 125 | 110 | 86 | 83 | 132 | 92 |
| 乙 | 108 | 116 | 89 | 123 | 126 | 113 |
| A. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,甲比乙成绩稳定 | B. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,乙比甲成绩稳定 | ||
| C. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,甲比乙成绩稳定 | D. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,乙比甲成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
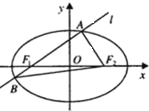 如图,椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$的左、右焦点分别为F1、F2,一条直线l经过F1与椭圆交于A,B两点,若直线l的倾斜角为45°,求△ABF2的面积.
如图,椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$的左、右焦点分别为F1、F2,一条直线l经过F1与椭圆交于A,B两点,若直线l的倾斜角为45°,求△ABF2的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com