
分析 (1)根据切点既在切线上又在函数f(x)的图象上,建立一等式关系,再根据导数的几何意义求出函数f(x)在x=2处的导数,建立另一关系式,解方程组即可求出a和b的值;
(2)先求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,即可求出函数的单调区间;
(3)由(2)即可求函数f(x)的极值.
解答 解:(1)∵切点(2,f(2))在切线y=8上,又f(2)=8-6a+b,
∴8-6a+b=8,得b=6a,①-------------------------------(2分)
∵f′(x)=3x2-3a,且y=f(x)在点(2,f(2))处的切线斜率为0,
∴f′(2)=12-3a=0,②---------------------------(4分)
由①②得,a=4,b=6a=24.------------------------------(5分)
(2)∵f(x)=x3-12x+24,∴f′(x)=3x2-12.
令f'(x)=0,则x=-2或2,-----------------------------(8分)
| x | (-∞,-2) | -2 | (-2,2) | 2 | (2,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 40 | 8 |
点评 本题是一综合题,考查了利用导数研究曲线上某点切线方程,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的极值.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:选择题
| 姓名/成绩 | 1 | 2 | 3 | 4 | 5 | 6 |
| 甲 | 125 | 110 | 86 | 83 | 132 | 92 |
| 乙 | 108 | 116 | 89 | 123 | 126 | 113 |
| A. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,甲比乙成绩稳定 | B. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,乙比甲成绩稳定 | ||
| C. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,甲比乙成绩稳定 | D. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,乙比甲成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
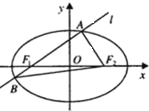 如图,椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$的左、右焦点分别为F1、F2,一条直线l经过F1与椭圆交于A,B两点,若直线l的倾斜角为45°,求△ABF2的面积.
如图,椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$的左、右焦点分别为F1、F2,一条直线l经过F1与椭圆交于A,B两点,若直线l的倾斜角为45°,求△ABF2的面积.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在x=e处取得极小值 | B. | 在x=e处取得极大值 | ||
| C. | 在x=$\frac{1}{e}$处取得极小值 | D. | 在x=$\frac{1}{e}$处取得极大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{25}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
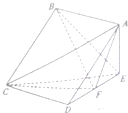 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com