
分析 推导出${{a}_{n}}^{2}-{{a}_{n-1}}^{2}$=$\frac{2{a}_{n}}{n}-\frac{1}{{n}^{2}}$,从而利用累加法,得${{a}_{n}}^{2}$=2(${a}_{1}+\frac{{a}_{2}}{2}+\frac{{a}_{3}}{3}+…+\frac{{a}_{n}}{n}$)-(1+$\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}+…+\frac{1}{{n}^{2}}$)+$\frac{7}{4}$,要证a${\;}_{n}^{2}$+$\frac{7}{4}>$2(a1$+\frac{{a}_{2}}{2}$$+\frac{{a}_{3}}{3}$$+…+\frac{{a}_{n}}{n}$)(n∈N*),只需证明:$1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}+…+\frac{1}{{n}^{2}}$<$\frac{7}{4}$,由此能证明a${\;}_{n}^{2}$+$\frac{7}{4}>$2(a1$+\frac{{a}_{2}}{2}$$+\frac{{a}_{3}}{3}$$+…+\frac{{a}_{n}}{n}$)(n∈N*).
解答 证明:∵an=1+$\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{n}$(n∈N*),
∴${a}_{n}={a}_{n-1}+\frac{1}{n}$,
∴(an-$\frac{1}{n}$)2=${{a}_{n-1}}^{2}$,
∴${{a}_{n}}^{2}-{{a}_{n-1}}^{2}$=$\frac{2{a}_{n}}{n}-\frac{1}{{n}^{2}}$,
${{a}_{n-1}}^{2}-{{a}_{n-2}}^{2}=\frac{2{a}_{n-1}}{n-1}-\frac{1}{(n-1)^{2}}$,
…
${{a}_{3}}^{2}-{{a}_{2}}^{2}$=$\frac{2{a}_{3}}{3}$-$\frac{1}{{3}^{2}}$,
${{a}_{2}}^{2}-{{a}_{1}}^{2}$=$\frac{2{a}_{2}}{2}-\frac{1}{{2}^{2}}$,
累加,得:${{a}_{n}}^{2}-{{a}_{1}}^{2}$=2($\frac{{a}_{2}}{2}+\frac{{a}_{3}}{3}+…+\frac{{a}_{n}}{n}$)-($\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}+…+\frac{1}{{n}^{2}}$),
∴${{a}_{n}}^{2}$=2(${a}_{1}+\frac{{a}_{2}}{2}+\frac{{a}_{3}}{3}+…+\frac{{a}_{n}}{n}$)-(1+$\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}+…+\frac{1}{{n}^{2}}$)+$\frac{7}{4}$,
要证a${\;}_{n}^{2}$+$\frac{7}{4}>$2(a1$+\frac{{a}_{2}}{2}$$+\frac{{a}_{3}}{3}$$+…+\frac{{a}_{n}}{n}$)(n∈N*),
只需证明:$1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}+…+\frac{1}{{n}^{2}}$<$\frac{7}{4}$,
n=1时,1<$\frac{7}{4}$;n=2时,1+$\frac{1}{{2}^{2}}$=$\frac{5}{4}$<$\frac{7}{4}$.
n≥3时,$1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}+…+\frac{1}{{n}^{2}}$<$1+\frac{1}{{2}^{2}}+\frac{1}{{2×3}^{\;}}$+$\frac{1}{3×4}+…+\frac{1}{n(n-1)}$
=1+$\frac{1}{4}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{n-1}-\frac{1}{n}$<$\frac{7}{4}$.
∴a${\;}_{n}^{2}$+$\frac{7}{4}>$2(a1$+\frac{{a}_{2}}{2}$$+\frac{{a}_{3}}{3}$$+…+\frac{{a}_{n}}{n}$)(n∈N*).
点评 本题考查数列不等式的证明,是中档题,解题时要认真审题,注意累加法、等价转化思想、放缩法、裂项求和法的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-3,-2} | C. | {-3,2} | D. | {-3,-2,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
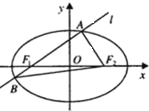 如图,椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$的左、右焦点分别为F1、F2,一条直线l经过F1与椭圆交于A,B两点,若直线l的倾斜角为45°,求△ABF2的面积.
如图,椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$的左、右焦点分别为F1、F2,一条直线l经过F1与椭圆交于A,B两点,若直线l的倾斜角为45°,求△ABF2的面积.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在x=e处取得极小值 | B. | 在x=e处取得极大值 | ||
| C. | 在x=$\frac{1}{e}$处取得极小值 | D. | 在x=$\frac{1}{e}$处取得极大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
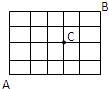 某城市的交通道路如图,从城市的东南角A到城市的西北角B,不经过十字道路维修处C,最近的走法种数有( )
某城市的交通道路如图,从城市的东南角A到城市的西北角B,不经过十字道路维修处C,最近的走法种数有( )| A. | 33 | B. | 60 | C. | 66 | D. | 126 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com