
分析 由已知中f(x)=-2x3+bx2+cx+d,当k<-1或k>4时,f(x)-k=0只有一个实根;当-1<k<4时,f(x)-k=0有三个相异实根,故函数即为极大值,又有极小值,且极大值为4,极小值为-1,分析出函数简单的图象和性质后,逐一分析四个结论的正误,即可得到答案.
解答 解:∵f(x)=-2x3+bx2+cx+d,f′(x)=-6x2+2bx+c,
当k<-1或k>4时,f(x)-k=0只有一个实根;
当-1<k<4时,f(x)-k=0有三个相异实根,
故函数既有极大值,又有极小值,且极大值为4,极小值为-1,
函数f(x)的图象先递减再递增再递减,
画出草图,如图示: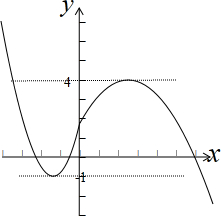 ,
,
f(x)-5=0的任一实根小于f(x)+5=0的任一实根,故①错误;
f(x)+2=0的任一实根大于f(x)-2=0的任一实根,故②正确;
f(x)-4=0与f'(x)=0有一个相同的实根,即极大值点,故③正确;
f(x)=-1与f'(x)=-1有一个相同的实根,即极小值点,故④错误;
故答案为:②③.
点评 本题考查的知识点是根的存在性及根的个数判断,其中根据已知条件,判断出函数f(x)=-2x3+bx2+cx+d的图象和性质是解答本题的关键.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$π | B. | $\frac{{\sqrt{2}}}{3}$π | C. | $\frac{{\sqrt{3}}}{2}$π | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
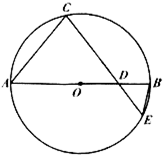 如图,AB是圆O的直径,弦CE交AB于D,CD=4$\sqrt{2}$,DE=$\sqrt{2}$,BD=2.
如图,AB是圆O的直径,弦CE交AB于D,CD=4$\sqrt{2}$,DE=$\sqrt{2}$,BD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com