
| A. | $\frac{4}{3}$π | B. | $\frac{{\sqrt{2}}}{3}$π | C. | $\frac{{\sqrt{3}}}{2}$π | D. | 3π |
分析 抓住正四面体的特征,底面是正三角形,边长为$\sqrt{2}$,高线的投影在底面正三角形的重心上.外接球的球心在高线上,且到各个顶点的距离相等,构造直角三角形,求出R,即可求球的体积.
解答 解: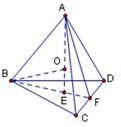
由题意:ABCD是正四面体,底面是正三角形,边长为$\sqrt{2}$,高线的投影在底面正三角形的重心上,则有BE=2EF;设AO=OB=R.
∵BCD是正三角形,边长为$\sqrt{2}$,
∴BF=$\sqrt{B{C}^{2}-C{F}^{2}}=\sqrt{2-(\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{6}}{2}$;
∴BE=$\frac{\sqrt{6}}{2}×\frac{2}{3}$=$\frac{\sqrt{6}}{3}$;
AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{2-\frac{2}{3}}=\frac{2\sqrt{3}}{3}$;
0E=AE-R=$\frac{2\sqrt{3}}{3}-R$
∵△BEO是直角三角形,
∴R2=OE2+BE2,即${R}^{2}=(\frac{2\sqrt{3}}{3}-R)^{2}+(\frac{\sqrt{6}}{3})^{2}$.
解得:R=$\frac{\sqrt{3}}{2}$,
则球的体积V=$\frac{4}{3}π{R}^{3}$
=$\frac{\sqrt{3}}{2}π$
故选:C.
点评 本题考查正四面体的特征以及球的体积的求法,解题时要认真审题,注意空间思维能力的培养.是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{7}\overrightarrow a+\frac{4}{7}\overrightarrow b$ | B. | $\frac{3}{7}\overrightarrow a-\frac{4}{7}\overrightarrow b$ | C. | $\frac{4}{7}\overrightarrow a+\frac{3}{7}\overrightarrow b$ | D. | $\frac{4}{7}\overrightarrow a-\frac{3}{7}\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<2} | B. | {x|x<-1或x≥2} | C. | {x|x≥2} | D. | {x|x<-1或x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0<x≤1} | D. | {x|0<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0° | B. | 60° | C. | 0°或60° | D. | 60°或90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-3,-2} | C. | {-3,2} | D. | {-3,-2,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2] | C. | (-∞,1] | D. | (-∞,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com