
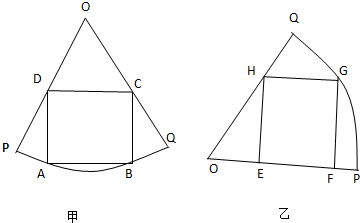
分析 乙方案根据构造辅助线,∠POG=θ,分别表示出EG和HG,根据矩形的面积公式求得S的表达式,根据三角恒等变换及正弦函数最值,即可求得S的最大值,对甲方案,构造辅助线,∠QOB=θ,表示出AB,根据正弦定理求得BC,根据矩形面积公式及正弦函数的最值,即可求得面积S,比较大小即可求得结果.
解答 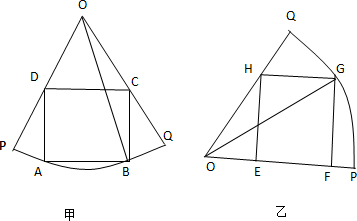 解:如图乙方案:设∠POG=θ,则FG=Rsinθ,
解:如图乙方案:设∠POG=θ,则FG=Rsinθ,
在△OEF中,HG=$\frac{2Rsin(60°-θ)}{\sqrt{3}}$,
又设矩形EFGH的面积为S,那么S=FG•HG=$\frac{2{R}^{2}sin(60°-θ)sinθ}{\sqrt{3}}$=$\frac{{R}^{2}}{\sqrt{3}}$•[cos(2θ-60°)-$\frac{1}{2}$],
又∵0°<θ<60°,故当cos(2θ-60°)=1,
即θ=30°时,S取最大$\frac{\sqrt{3}}{6}$R2;
如图甲方案,设∠QOB=θ,则AB=2Rsin(30°-θ),在△OFG中,∠OCB=150°,
$\frac{BC}{sinθ}$=$\frac{R}{sin150°}$,即BC=2Rsinθ
设矩形的面积为S.
那么SEFFG=4R2sinθsin(30°-θ)
=2R2[cos(2θ-30°)-cos30°]=2R2[cos(2θ-30°)-$\frac{\sqrt{3}}{2}$],
又∵0<θ<30°,故当cos(2θ-30°)=1即θ=15°时,S取最大R2(2-$\sqrt{3}$),
显然$\frac{\sqrt{3}}{6}$R2>R2(2-$\sqrt{3}$),
乙方案矩形的最大面积.
点评 本题考查三角恒等变换的实际应用,考查正弦函数最值及正弦定理的应用,考查计算能力,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2] | C. | (-∞,1] | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
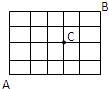 某城市的交通道路如图,从城市的东南角A到城市的西北角B,不经过十字道路维修处C,最近的走法种数有( )
某城市的交通道路如图,从城市的东南角A到城市的西北角B,不经过十字道路维修处C,最近的走法种数有( )| A. | 33 | B. | 60 | C. | 66 | D. | 126 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
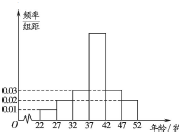 为了解游客对2015年“十一”小长假的旅游情况是否满意,某旅行社从年龄(单位:岁)[22,52]在内的游客中随机抽取了1000人,并且作出了各个年龄段的频率分布直方图如图所示,同时对这1000人的旅游结果满意情况进行统计得到如表:
为了解游客对2015年“十一”小长假的旅游情况是否满意,某旅行社从年龄(单位:岁)[22,52]在内的游客中随机抽取了1000人,并且作出了各个年龄段的频率分布直方图如图所示,同时对这1000人的旅游结果满意情况进行统计得到如表:| 分组 | 满意的人数 | 占本组的频率 |
| [22,27) | 30 | 0.6 |
| [27.32) | n | 0.95 |
| [32,37) | 120 | 0.8 |
| [37,42) | 432 | m |
| [42,47) | 144 | 0.96 |
| [47,52) | 96 | 0.96 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
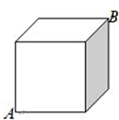 如图是边长为1的正方体,有一蜘蛛潜伏在A处,B处有一小虫被蜘蛛网粘住,请问蜘蛛从A到B正方体表面爬行的最短路程为( )
如图是边长为1的正方体,有一蜘蛛潜伏在A处,B处有一小虫被蜘蛛网粘住,请问蜘蛛从A到B正方体表面爬行的最短路程为( )| A. | 3 | B. | $\sqrt{2}$+1 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com