
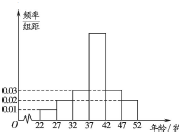
 为了解游客对2015年“十一”小长假的旅游情况是否满意,某旅行社从年龄(单位:岁)[22,52]在内的游客中随机抽取了1000人,并且作出了各个年龄段的频率分布直方图如图所示,同时对这1000人的旅游结果满意情况进行统计得到如表:
为了解游客对2015年“十一”小长假的旅游情况是否满意,某旅行社从年龄(单位:岁)[22,52]在内的游客中随机抽取了1000人,并且作出了各个年龄段的频率分布直方图如图所示,同时对这1000人的旅游结果满意情况进行统计得到如表:| 分组 | 满意的人数 | 占本组的频率 |
| [22,27) | 30 | 0.6 |
| [27.32) | n | 0.95 |
| [32,37) | 120 | 0.8 |
| [37,42) | 432 | m |
| [42,47) | 144 | 0.96 |
| [47,52) | 96 | 0.96 |
分析 (1)根据题意可得,年龄在[37,42)内的频率为1-(0.01+0.02×2+0.03×2)×5,即可得出年龄在[37,42)内的人数及其m.年龄在[27,32)内的频率为0.02×5,即可得出n.
(2)由题意采用分层抽样的方法抽取的10人中,年龄在[42,47)内且满意的人数与年龄在[47,52]内且满意的人数分别为6,4.依题意可得X=0,1,2,3,4.利用古典概率计算公式、超几何分布列及其数学期望的计算公式即可得出.
解答 解:(1)根据题意可得,年龄在[37,42)内的频率为1-(0.01+0.02×2+0.03×2)×5=0.45,
故年龄在[37,42)内的人数为450,则$m=\frac{432}{450}=0.96$,
年龄在[27,32)内的人数为1000×0.02×5=100,
故n=100×0.95=95.
(2)因为年龄在[42,47)内且满意的人数为员144,年龄在[47,52]内且满意的人数为96,因此采用分层抽样的方法抽取的10人中,年龄在[42,47)内且满意的人数与年龄在[47,52]内且满意的人数分别为6,4.
依题意可得X=0,1,2,3,4.
$P(X=0)=\frac{C_6^4C_4^0}{{C_{10}^4}}=\frac{15}{210}=\frac{1}{14};P(X=1)=\frac{C_6^3C_4^1}{{C_{10}^4}}=\frac{80}{210}=\frac{8}{21};P(X=2)=\frac{C_6^2C_4^2}{{C_{10}^4}}=\frac{90}{210}=\frac{3}{7}$$P(X=3)=\frac{C_6^1C_4^3}{{C_{10}^4}}=\frac{24}{210}=\frac{4}{35};P(X=4)=\frac{C_6^0C_4^4}{{C_{10}^4}}=\frac{1}{210}$.X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{14}$ | $\frac{8}{21}$ | $\frac{3}{7}$ | $\frac{4}{35}$ | $\frac{1}{210}$ |
点评 本题考查了频率分布直方图的性质及其应用、古典概率计算公式、超几何分布列及其数学期望的计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=(x-a)|x|,a≠0 | B. | f(x)=x2+ax+1,a∈R | C. | f(x)=log2(ax-1),a∈R | D. | f(x)=ax2+cosx,a∈R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 级数 | 全月应纳税所得额 | 税率(%) |
| 1 | 不超过1500元 | 3 |
| 2 | 1500元-4500元 | 10 |
| A. | 7000元 | B. | 7500元 | C. | 6600元 | D. | 5950元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com