
| A. | f(x)=(x-a)|x|,a≠0 | B. | f(x)=x2+ax+1,a∈R | C. | f(x)=log2(ax-1),a∈R | D. | f(x)=ax2+cosx,a∈R |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
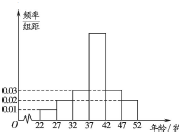 为了解游客对2015年“十一”小长假的旅游情况是否满意,某旅行社从年龄(单位:岁)[22,52]在内的游客中随机抽取了1000人,并且作出了各个年龄段的频率分布直方图如图所示,同时对这1000人的旅游结果满意情况进行统计得到如表:
为了解游客对2015年“十一”小长假的旅游情况是否满意,某旅行社从年龄(单位:岁)[22,52]在内的游客中随机抽取了1000人,并且作出了各个年龄段的频率分布直方图如图所示,同时对这1000人的旅游结果满意情况进行统计得到如表:| 分组 | 满意的人数 | 占本组的频率 |
| [22,27) | 30 | 0.6 |
| [27.32) | n | 0.95 |
| [32,37) | 120 | 0.8 |
| [37,42) | 432 | m |
| [42,47) | 144 | 0.96 |
| [47,52) | 96 | 0.96 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{43}{128}$ | B. | $\frac{43}{64}$ | C. | $\frac{13}{128}$ | D. | $\frac{13}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com