
分析 (1)由题意求得转换矩阵M,由,则$[{\begin{array}{l}1&0\\ 0&5\end{array}}][{\begin{array}{l}x\\ y\end{array}}]=[{\begin{array}{l}{x'}\\{y'}\end{array}}]$,求得$\left\{{\begin{array}{l}{x'=x}\\{y'=5y}\end{array}}\right.$,代入直线4x-10y=1方程,即可求得方程M作用下的方程;
(2)令特征多项式f(λ)=0,求得特征值,将特征值代入即可求得特征向量;
(3)由$[\begin{array}{l}2\\ 3\end{array}]=2{α_1}+3{α_2}$,则${M^5}[\begin{array}{l}2\\ 3\end{array}]=2×{1^5}[{\begin{array}{l}1\\ 0\end{array}}]+3×{5^5}[{\begin{array}{l}0\\ 1\end{array}}]=[\begin{array}{l}2\\ 3•{5^5}\end{array}]$.
解答 解:(1)由题意可知:变换矩阵M,$M=[{\begin{array}{l}1&0\\ 0&5\end{array}}]$,
设(x',y')是所求曲线上的任一点,则$[{\begin{array}{l}1&0\\ 0&5\end{array}}][{\begin{array}{l}x\\ y\end{array}}]=[{\begin{array}{l}{x'}\\{y'}\end{array}}]$,所以$\left\{{\begin{array}{l}{x'=x}\\{y'=5y}\end{array}}\right.$
从而$\left\{{\begin{array}{l}{x=x'}\\{y=\frac{1}{5}y'}\end{array}}\right.$代入4x-10y=1得,4x'-2y'-1=0,
∴曲线的方程为4x-2y-1=0.--------------------(4分)
(2)矩阵M的特征多项式$f(λ)=|{\begin{array}{l}{λ-1}&0\\ 0&{λ-5}\end{array}}|=(λ-1)(λ-5)$,
由f(λ)=0得,矩阵M的特征值为λ1=1,λ2=5.(6分)
当λ1=1时,对应的一个特征向量${α_1}=[{\begin{array}{l}1\\ 0\end{array}}]$;
当λ2=5时,对应的一个特征向量${α_2}=[{\begin{array}{l}0\\ 1\end{array}}]$.------------------------(8分)
(3)∵$[\begin{array}{l}2\\ 3\end{array}]=2{α_1}+3{α_2}$,
∴${M^5}[\begin{array}{l}2\\ 3\end{array}]=2×{1^5}[{\begin{array}{l}1\\ 0\end{array}}]+3×{5^5}[{\begin{array}{l}0\\ 1\end{array}}]=[\begin{array}{l}2\\ 3•{5^5}\end{array}]$.-----------------------(10分)
点评 本题考查矩阵的变换,考查矩阵的特征向量及特征向量,矩阵的乘法运算,考查计算能力,属于中档题.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:解答题
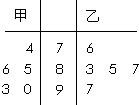 甲、乙两名同学在5次英语口语测试中的成绩统计如下面的茎叶图所示.
甲、乙两名同学在5次英语口语测试中的成绩统计如下面的茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=(x-a)|x|,a≠0 | B. | f(x)=x2+ax+1,a∈R | C. | f(x)=log2(ax-1),a∈R | D. | f(x)=ax2+cosx,a∈R |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com