
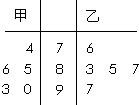
 甲、乙两名同学在5次英语口语测试中的成绩统计如下面的茎叶图所示.
甲、乙两名同学在5次英语口语测试中的成绩统计如下面的茎叶图所示.分析 (Ⅰ)计算甲乙的平均数与方差,即可得出结论.
(Ⅱ)用列举法求得从甲的这5次测试成绩中抽取2次,全部可能的基本结果有10个,而所求事件包括2个基本事件,由此求得所求事件的概率.
解答 解:(Ⅰ)$\overline{{x}_{甲}}$=$\frac{74+85+86+90+93}{5}$=85.6,$\overline{{x}_{乙}}$=$\frac{76+83+85+97+97}{5}$=85.6
Dx甲=$\frac{1}{5}$[(74-85.6)2+(85-85.6)2+(86-85.6)2+(90-85.6)2+(93-85.6)2]=41.84;
Dx乙=$\frac{1}{5}$[(76-85.6)2+(83-85.6)2+(85-85.6)2+(87-85.6)2+(97-85.6)2]=46.24;
∵Dx甲<Dx乙,
∴甲的水平更稳定,所以派甲去;
(Ⅱ)取得的样本情况为:(74,85),(74,86),(74,90),(74,93),(85,86),(85,90)
(85,93),(86,90),(86,93),(90,93)
样本平均数分别为:79.5,80,82,83.5,85.5,87.5,89,88,89.5,91.5
与总体平均数86.5距离不超过2的有85.5,87.5两个,故P=$\frac{2}{10}$=$\frac{1}{5}$.
点评 本题考主要查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法,属于基础题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|x<2} | B. | {x|x<-1或x≥2} | C. | {x|x≥2} | D. | {x|x<-1或x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0<x≤1} | D. | {x|0<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0° | B. | 60° | C. | 0°或60° | D. | 60°或90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com