
分析 利用同角的三角函数关系,把正弦、余弦的比值化为正切tanα,即可求出各式的值.
解答 解:由于:tanα=2,
(1)$\frac{2sinα+cosα}{5sinα-3cosα}$=$\frac{2tanα+1}{5tanα-3}$=$\frac{2×2+1}{5×2-3}$=$\frac{5}{7}$;
(2)$\frac{2si{n}^{2}α-3sinα•cosα}{4si{n}^{2}α-7co{s}^{2}α}$=$\frac{2ta{n}^{2}α-3tanα}{4ta{n}^{2}α-7}$=$\frac{2×{2}^{2}-3×2}{4×{2}^{2}-7}$=$\frac{2}{9}$;
(3)$\frac{3}{4}$sin2α+$\frac{2}{5}$cos2α=$\frac{\frac{3}{4}si{n}^{2}α+\frac{2}{5}co{s}^{2}α}{si{n}^{2}α+co{s}^{2}α}$=$\frac{\frac{3}{4}ta{n}^{2}α+\frac{2}{5}}{ta{n}^{2}α+1}$=$\frac{\frac{3}{4}×{2}^{2}+\frac{2}{5}}{{2}^{2}+1}$=$\frac{17}{25}$.
点评 本题考查了同角的三角函数关系的应用问题,考查了转化思想,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题

| A. | 直线AB上 | B. | 直线BC上 | C. | 直线AC上 | D. | △ABC内部 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
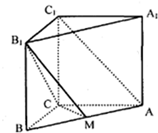 如图,直三棱柱ABC-A1B1C1中,AC=BC=AA1=3,AC⊥BC,点M在线段AB上.
如图,直三棱柱ABC-A1B1C1中,AC=BC=AA1=3,AC⊥BC,点M在线段AB上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
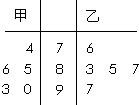 甲、乙两名同学在5次英语口语测试中的成绩统计如下面的茎叶图所示.
甲、乙两名同学在5次英语口语测试中的成绩统计如下面的茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com