
分析 将函数利用二倍角公式和辅助角公式进行化简,结合三角函数的图象和性质即可得出答案.
解答 解:f(x)=sin(x+$\frac{π}{6}$)+cos2$\frac{x}{2}$,
=sinxcos$\frac{π}{6}$+cosxsin$\frac{π}{6}$+$\frac{1}{2}$cosx+$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}sinx$+$\frac{1}{2}$cosx+$\frac{1}{2}$cosx+$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}sinx$+cosx+$\frac{1}{2}$
=$\frac{\sqrt{7}}{2}$sin(x+φ)+$\frac{1}{2}$,其中tanφ=$\frac{2\sqrt{3}}{3}$;
∴振幅为$\frac{\sqrt{7}}{2}$,最小正周期T=$\frac{2π}{|ω|}=\frac{2π}{1}=2π$;
故答案为$\frac{\sqrt{7}}{2}$,2π.
点评 本题考查了利用二倍角公式和辅助角公式进行三角函数的能力和三角函数的图象和性质的运用.属于基础题


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 在x=e处取得极小值 | B. | 在x=e处取得极大值 | ||
| C. | 在x=$\frac{1}{e}$处取得极小值 | D. | 在x=$\frac{1}{e}$处取得极大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
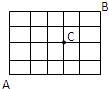 某城市的交通道路如图,从城市的东南角A到城市的西北角B,不经过十字道路维修处C,最近的走法种数有( )
某城市的交通道路如图,从城市的东南角A到城市的西北角B,不经过十字道路维修处C,最近的走法种数有( )| A. | 33 | B. | 60 | C. | 66 | D. | 126 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
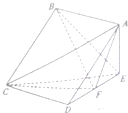 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
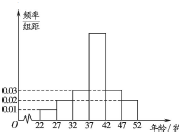 为了解游客对2015年“十一”小长假的旅游情况是否满意,某旅行社从年龄(单位:岁)[22,52]在内的游客中随机抽取了1000人,并且作出了各个年龄段的频率分布直方图如图所示,同时对这1000人的旅游结果满意情况进行统计得到如表:
为了解游客对2015年“十一”小长假的旅游情况是否满意,某旅行社从年龄(单位:岁)[22,52]在内的游客中随机抽取了1000人,并且作出了各个年龄段的频率分布直方图如图所示,同时对这1000人的旅游结果满意情况进行统计得到如表:| 分组 | 满意的人数 | 占本组的频率 |
| [22,27) | 30 | 0.6 |
| [27.32) | n | 0.95 |
| [32,37) | 120 | 0.8 |
| [37,42) | 432 | m |
| [42,47) | 144 | 0.96 |
| [47,52) | 96 | 0.96 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②④ | B. | ①③ | C. | ②③④ | D. | ①②③④⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com